数字逻辑
二进制
名词解释
三Y原则:
层次化:hierarchy
模块化:modularity
规整化:regularity
其他:
抽象:abstraction
约束:discipline
二进制:
半字节:nibble:4位
字节:byte:8位
最高有效位/字节:msb/MSB
最低有效位/字节:lsb/LSB
bps:bit per second
计算
其他进制转换为十进制
//二进制下转化: |
二进制加减
//无符号 |
补位
//带符号二进制下 |
表示范围
//无符号 |
逻辑门
非门,缓冲器,与门,非门
逻辑图等下节给出
噪声容限
输出为离散的最高值(1)或最低值(0),但产生波动
输入为输出后的波动值加噪声容限
禁止区域内既不能高电压接收,又不能低电压接收。—————具体见p14.1-12
习题
- 无符号的n位二进制的表示范围:$(0,2^N-1)$
- 有符号的n位二进制表示范围:$(-(2^{n-1}-1),2^{n-1}-1)$
- 二进制补码(n位)的表示范围:$(-2^{n-1},2^{n-1}-1)$
- 无符号二进制转十进制到转其他其他进制或互转
- 补码转十进制:补码先取反加一转换为原码,再转换为十进制
- 十进制转化为二进制补码(自带符号):你肯定会
- 二进制补码的扩展:
以1010为例,-》1110为原码-》10000110为扩展后原码-》得到答案- 八进制,十六进制,二进制的互转
8-2
以32为例,从右往左看,2->010,3->011,此处为三位,反转时也一致
16-2
以32为例,从右往左,2->0010,3->0011,此处为4位,- 无符号二进制加法和二进制补码加法
- 一些偏题,日后说
(1)偏置量:10进制转二进制要加上偏置量,二进制转十进制要减去偏置量
(2)BCD转码(1.65)
(3)余下一些有关噪声容限的题目,有些抽象,不看了- 考察各种门的符号,真值表
组合逻辑设计
组合电路设计与真值表
名词:
元件:element:带有输入输出,功能规范,时序规范的电路。
节点:node:导线
数字电路:组合电路(combinational circuit)+时序电路(sequential circult)
组合电路设计
要求:无回路,电路节点只能是输入或输出,电路元件本身是组合电路
真值表
NAND3
| A | B | C | Y |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
XOR3(全加器)
| A | B | Cin | Y | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
n输入就有2^n种情况
逻辑电路式
与或式
给出随机一真值表
| A | B | Y | minterm | minterm name |
|---|---|---|---|---|
| 0 | 0 | 1 | $\bar a$ $\bar b$ | m0 |
| 1 | 1 | 0 | ab | m1 |
| 0 | 1 | 0 | $\bar a$b | m2 |
| 1 | 0 | 1 | a$\bar b$ | m3 |
minterm项为使AND为1的方法,name从0开始排
得到Y=$\bar a$ $\bar b$ +a $\bar b$
(选取Y为1的项相加)
或于式
如上,给出一表
| A | B | Y | maxterm | maxterm name |
|---|---|---|---|---|
| 0 | 0 | 1 | a+b | m0 |
| 1 | 1 | 0 | $\bar a$+$\bar b$ | m1 |
| 0 | 1 | 0 | a+$\bar b$ | m2 |
| 1 | 0 | 1 | $\bar a$+b | m3 |
maxterm项为使OR为0的方法,name从0开始排
得到Y=(a+b)($\bar a$+b)
(选取Y为0的项相乘)
布尔代数
特殊运算
| b*1=b | b*b=b |
|---|---|
| b+1=1 | b+b=b |
| b*${\bar b}$=0 | b+${\bar b}$=1 |
| a(b+c)=ab+ac | (b+c)(b+d)=b+cd |
| b(b+c)=b+bc=b | b+bc=b+1/b+0=b |
| bc+${\bar b}$d+cd=bc+$\bar b$d | (b+c)(${\bar b}$+d)(c+d)=(b+c)(${\bar b}$+d) |
德摩根定理
| ${\overline{abc}=\bar a+\bar b+\bar c}$ | ${\overline{a+b+c}=\bar a\bar b\bar c}$ |
|---|---|
电路原理图
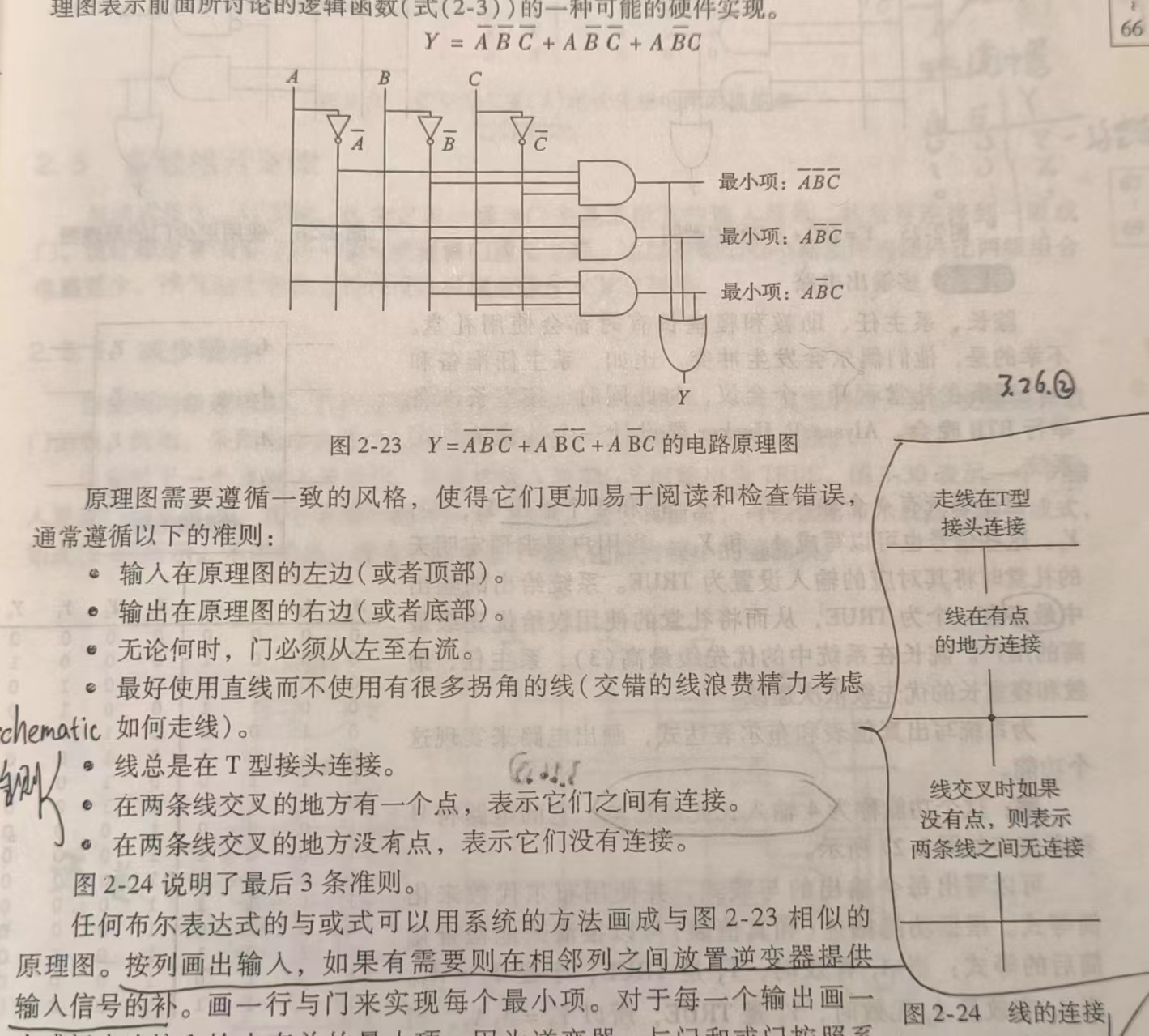
其中,左上角为缓冲器及其反,右下角为输出。
交叉直线见图
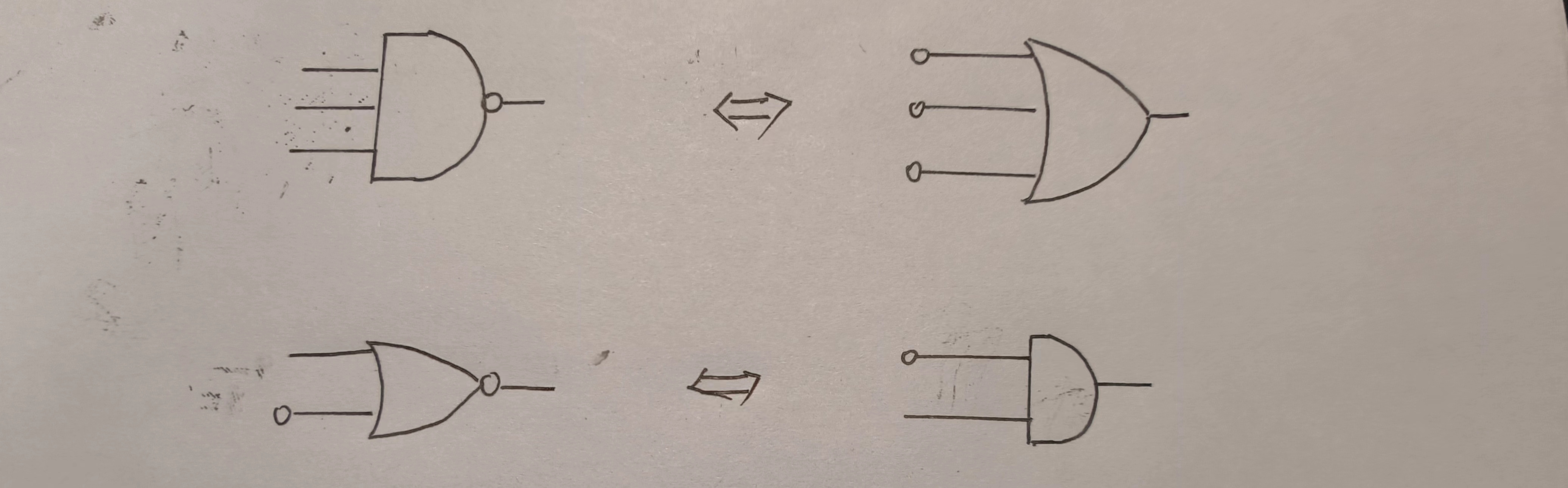
推气泡法
该法为快速消去反,实现化简。
见图如下
特殊电路
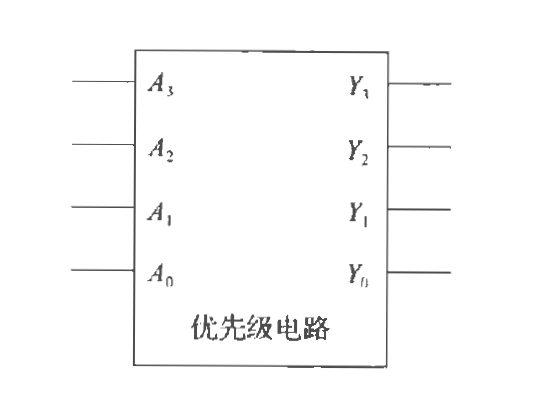
优先级电路

| $A_3$ | $A_2$ | $A_1$ | $A_0$ | $Y_3$ | $Y_2$ | $Y_1$ | $Y_0$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 | 0 |
| 0 | 1 | x | x | 1 | 0 | 0 | 0 |
| 1 | x | x | x | 1 | 1 | 0 | 0 |
优先级:$A_3>A_2>A_1$,故其他小位不对大位构成影响
有表达式$Y_3=A_3+A_2$
$Y_2=A_3+\bar{A_2}A_1$
$Y_1=\overline{A_3A_2}A_1$
$Y_0=\overline{A_3A_2A_1}A_0$
可见:表达式也具有优先属性
(x可取任意值)
使能信号
在缓冲器上增加一输入,该输入控制原本的输入
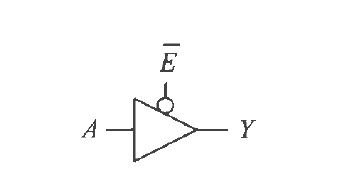
如E
有真值表
| $\overline E$ | $A$ | $Y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | z |
| 1 | 1 | z |
z表示浮动值,既可以是0,也可以是1,或是无关紧要的值.当E为0时,通道打开,A的信号传入Y
译码器
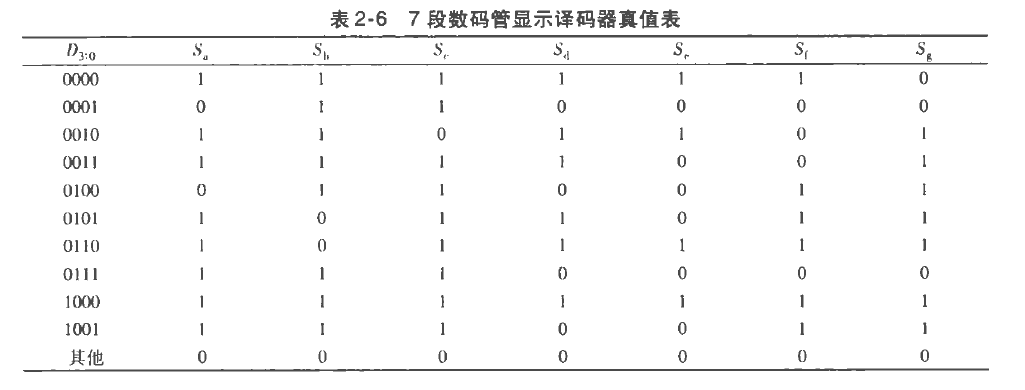
共十种输出,对应7个电子管,点亮得到数字图案,其他的输出时无关紧要的
卡诺图
最小项卡诺图
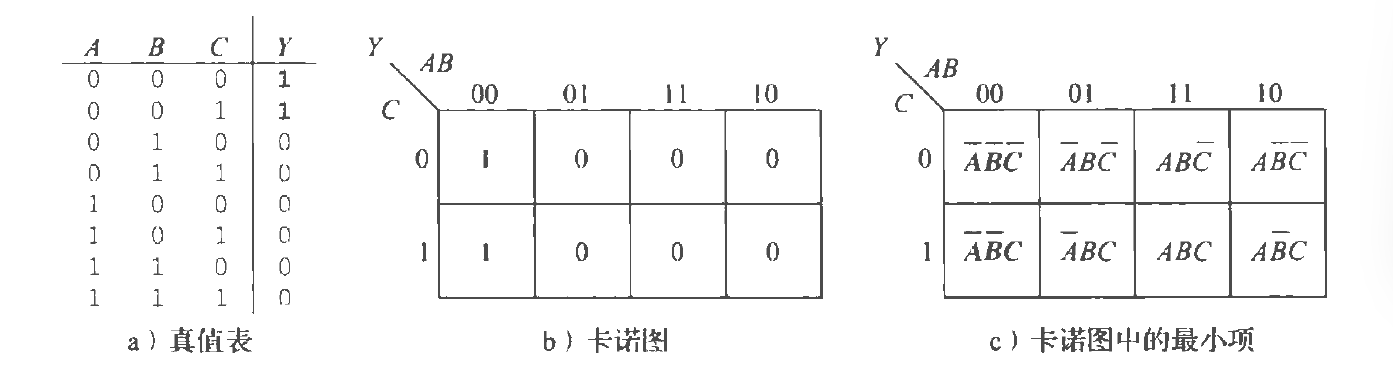
注意
1.用最小项的写法
2.圈要大,少
3.表是循环的,如上图AB栏,00左边延续10,1下面延续0等
3.圈内元素为2的n次幂,如:1,2,4,8等
4.边角4个可以组成一个圈
复用器
2:1复用器
复用器的数量:$n=log_2n_d$
| S | $D_1$ | $D_2$ | $Y$ |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
s作为选择信号,为1时打开$D_1$,为0时打开$D_2$
对一复用器真值表,既可按表正选,也可缩写
对$Y=A\bar B+\overline BC +\bar A BC$,有
| A | B | C | $Y$ |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
或缩写
| AB | Y |
|---|---|
| 00 | $\overline C$ |
| 01 | C |
| 10 | 1 |
| 11 | 0 |
或缩写
| A | Y |
|---|---|
| 0 | $\overline {BC}+BC$ |
| 0 | $\overline B$ |

例如,在图a中A为0时输入接地,为0;A为1时输入为B。
译码器
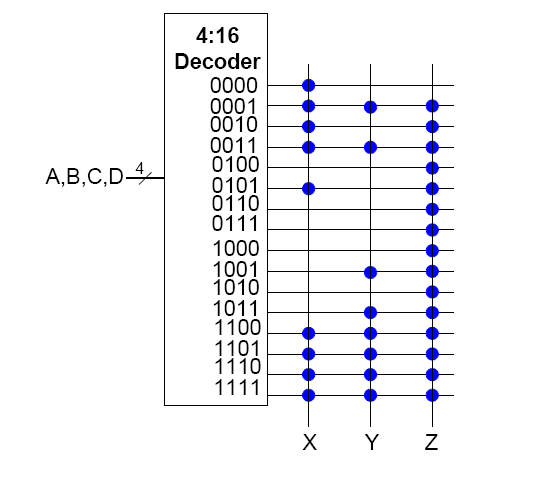
直接得到最小项的组合,据此组合得到各种组合电路
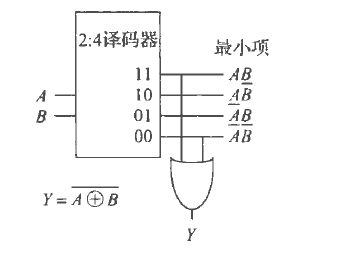
得到$2^n$个输出子电路,随后就可以进行组合,只需要两个元件
有如下真值表(3:8)
时序
延迟时间
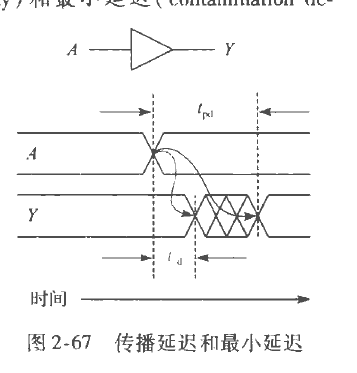
输入改变引发输出改变,但存在延迟
$T_{cd}$为最小延迟:输出快速变为输入水平的时间
$T_{pd}$为传播延迟(最大延迟):输出在经历摇摆后稳定到输入水平的时间
延迟计算
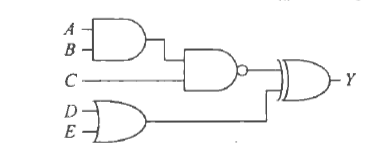
从A-E五个输入中找到通往输出的最短路($T_{cd}$),和最长路($T_{pd}$)。
如上图
左侧标黑为最长路,路上有两个输入,A,B。
路上三个门,$T=T_{pd}AND + T_{pd}NAND+T_{pd}XOR$
右侧标黑为最短路,路上三个输入,C,D,E
路上两个门,$T=T_{cd}OR+T_{cd}XOR$或$T=T_{cd}NAND+T_{cd}XOR$
为什么说两个门,因为C,D和E是同时过的,所以我用了或。
—————————————————————————————————————————p53有未提及的难点
毛刺
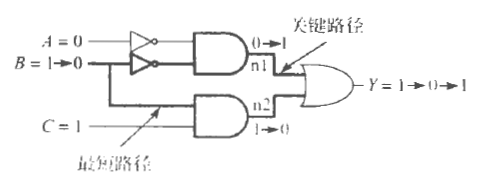
当B由1变为0时,由于$T_{cd}$和$T_{pd}$,导致输入传来的时间不一样,导致Y出现了中间值0
习题
- 布尔表达式
最小项:
与或
使乘积为1,取值为1
最大项:
或与
使和为0,取值为0- 布尔定理化简
讲究做题,考试时再看- 布尔表达式化简:
需要最小项卡诺图,2^n个元素为准
4.情景题(或要求题):要么直接得到答案,要么列出真值表- 复用器(switch()),也有写出复用器代表的布尔表达式,此处建议使用卡诺图化简,大佬可以一眼看出组合
- 译码器:由输入组合得到各种电路
- 计算延时:最常长路用$T_{pd}$,最短路用$T_{cd}$,此处可能需要注意
时序逻辑设计
锁存器和触发器
双稳态元件
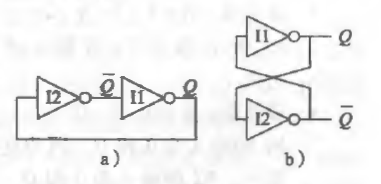
无论假定Q是多少,其值都会在电路内循环,保持不变,用户无法改变电路内情况
SR锁存器
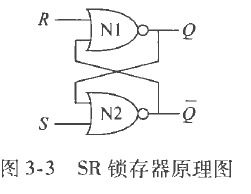
该电路相对于双稳态元件,额外增加了两个输入,即允许用户修改其内部的信号。
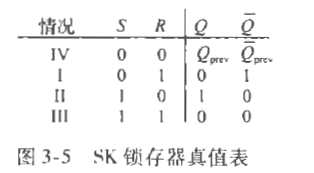
S R都为0时,电路状态不变。都为1时,锁存器的两端电路不能同时被重铸,导致陷入混乱,即没有意义。
D锁存器

引入了$CLK$时钟,当时钟为1时,D的值将直接赋给Q,另一个输出自然取反。
当时钟为0时,SR锁存器保持原值。
D触发器
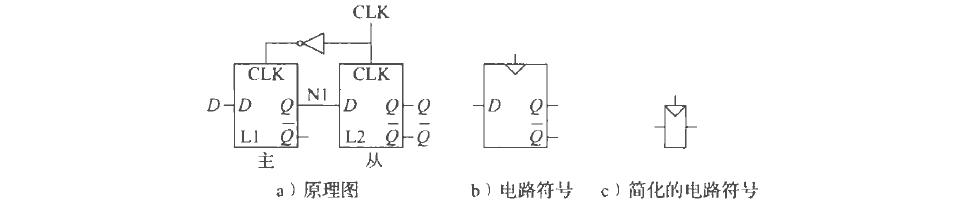
类似于两节管子,CLK为1时主SR不接受输入,从接受但N1无输出(或输出不变)。CLK为0时,主打开,D存储在N1,随后若CLK变为1,那么N1就会赋给Q,同时主关闭。相当于存储了一段信息在N1中
相当于只传递了Q,因为D—0-1—-,Q———-0—1—。
寄存器
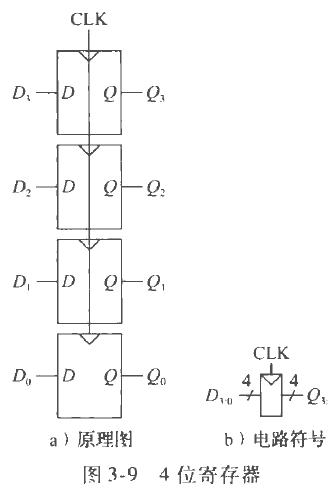
为D触发器的简单组合。
储存器的变型
带使能端的触发器
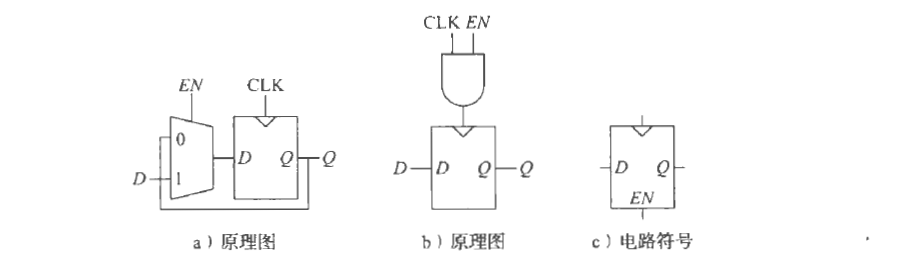
当EN为0时,跳过CLK,直接为Q赋值。反之则为正常流程
带复位功能的触发器
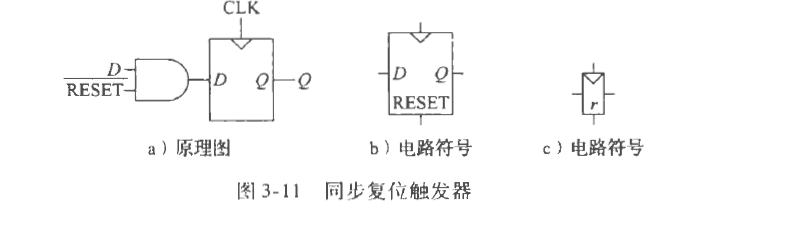
RESET为FALSE时,复位Q为0
解的波形
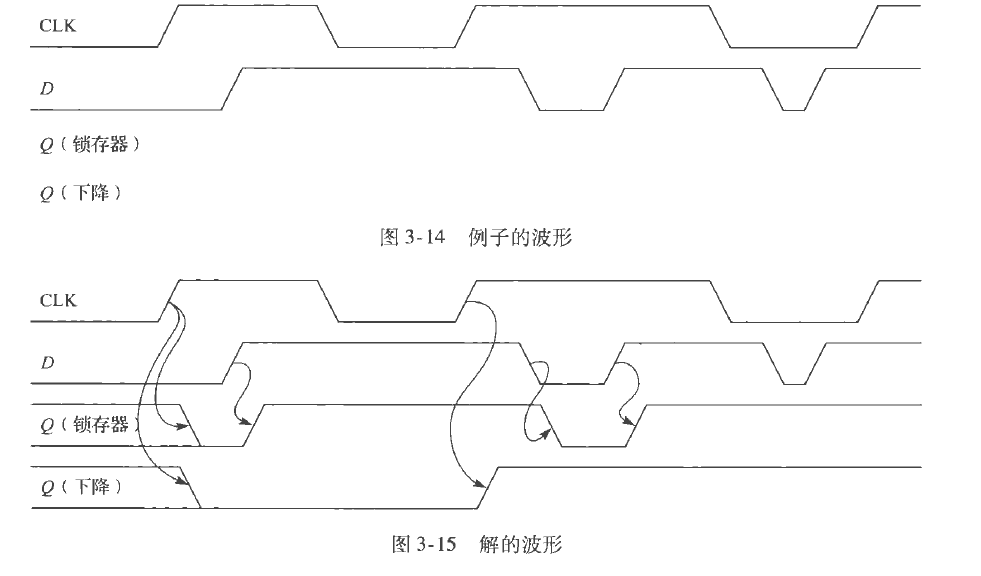
要点:
- CLK和D对Q(D锁存器)和Q(D触发器)都有时间延迟
- 两个Q的功能各有不同,注意分辨
- 两个Q前期值不确定,画成两条线
- 延迟箭头由变化的CLK和D引起,所以存在有时只画一条箭头的情况
- CLK在上升期使得Q(D触发器)的取值变为Q(锁存器)
- D使得Q(锁存器改变)
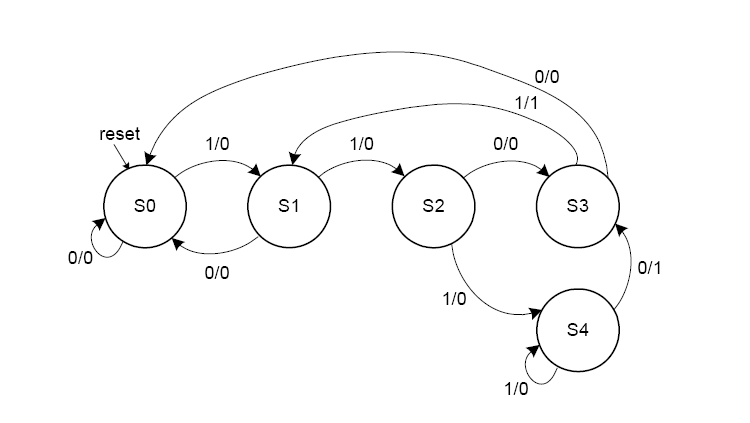
有限状态机
moore型有限状态机
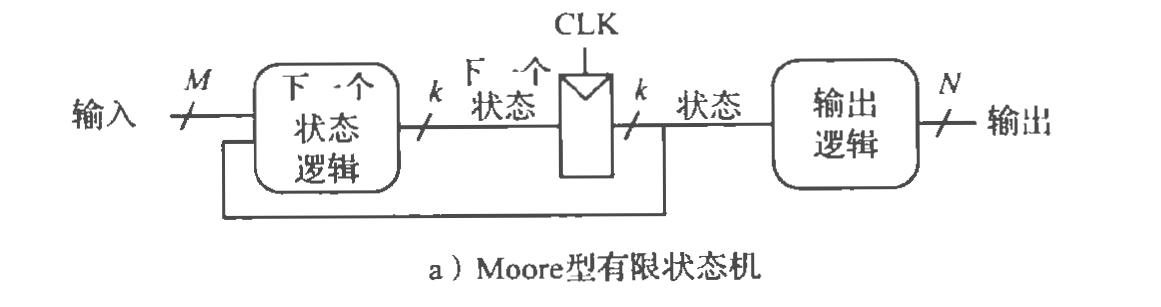
状态逻辑由当前状态和输入决定
输出逻辑由当前状态决定
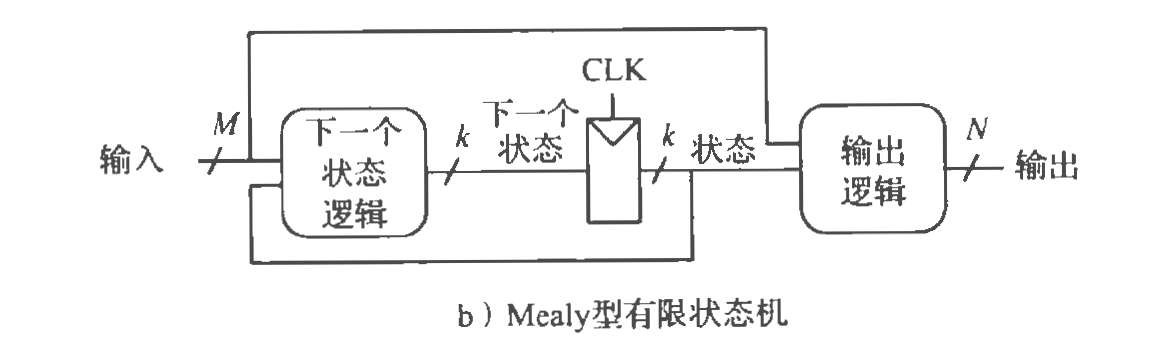
状态逻辑由当前状态和输入共同决定
输出逻辑由当前状态和输入共同决定
有限状态机的设计
例一
十字路口策略。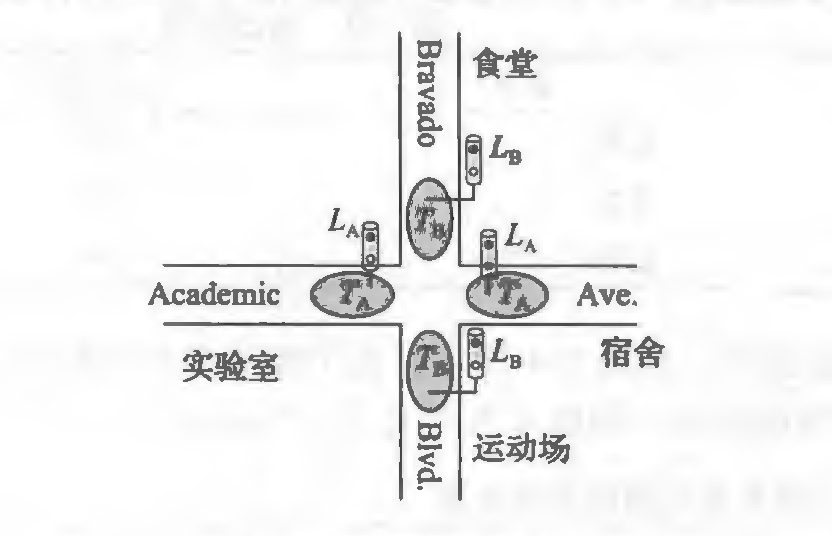
对A,B两地,有$T_A,T_B$两个输入,为TRUE时,表示有人,原状态不变,否则改变。
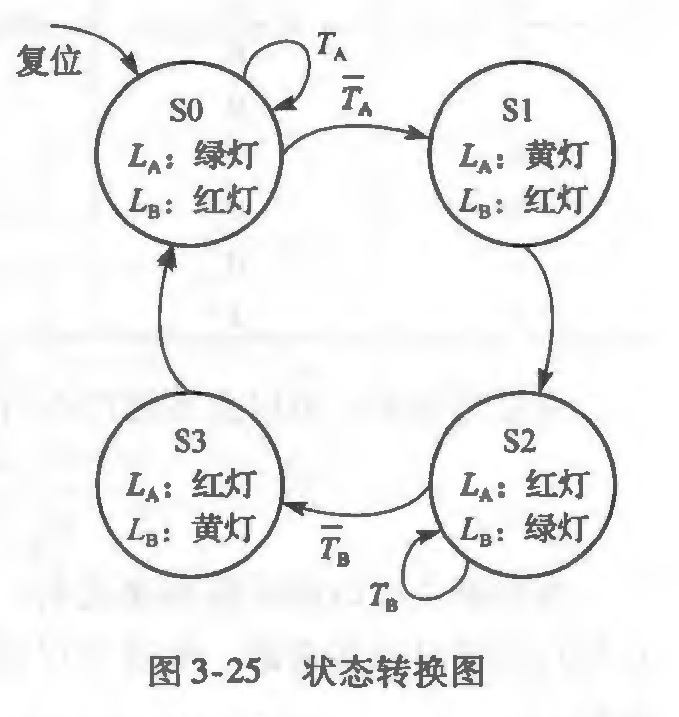
得到状态转换图:
由此
| $S$ | $T_A$ | $T_B$ | $S^`$ |
|---|---|---|---|
| s0 | 1 | x | s0 |
| s0 | 0 | x | s1 |
| s1 | x | x | s2 |
| s2 | x | 1 | s2 |
| s2 | x | 0 | s3 |
| s3 | x | x | s0 |
得到状态逻辑的逻辑编码(二进制)
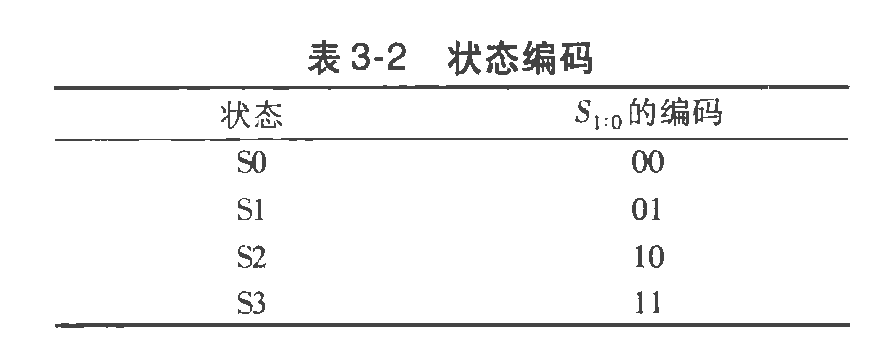
及对应真值表

可得到$S^_1,S^_2$的公式
其中,若关于$S_1,S_2$的所有组合都完善且对应与输入的组合都存在,即无需补充时,化简即可,反之可补充,部分值设为x,添加后化简。
同理:得到输出逻辑的逻辑编码(二进制)

和
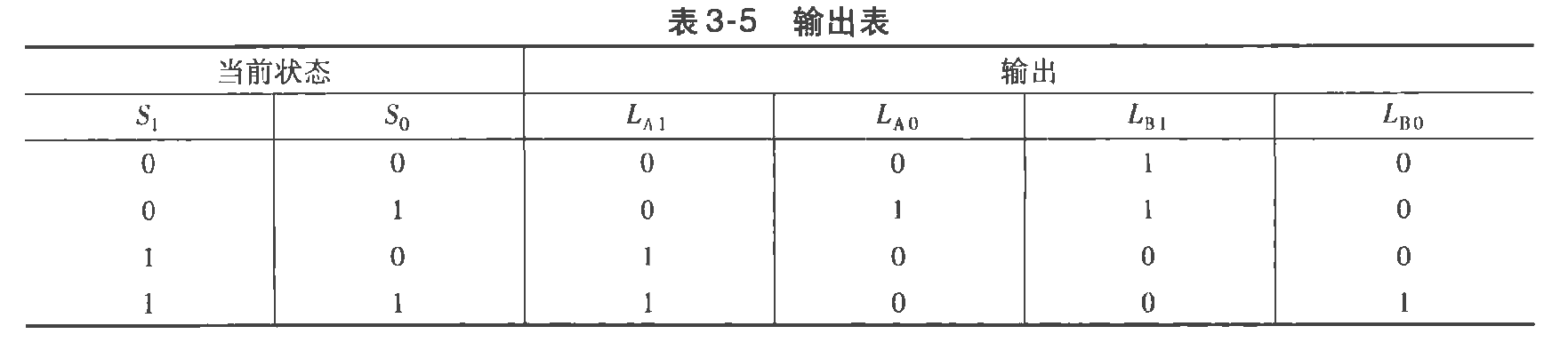
得到
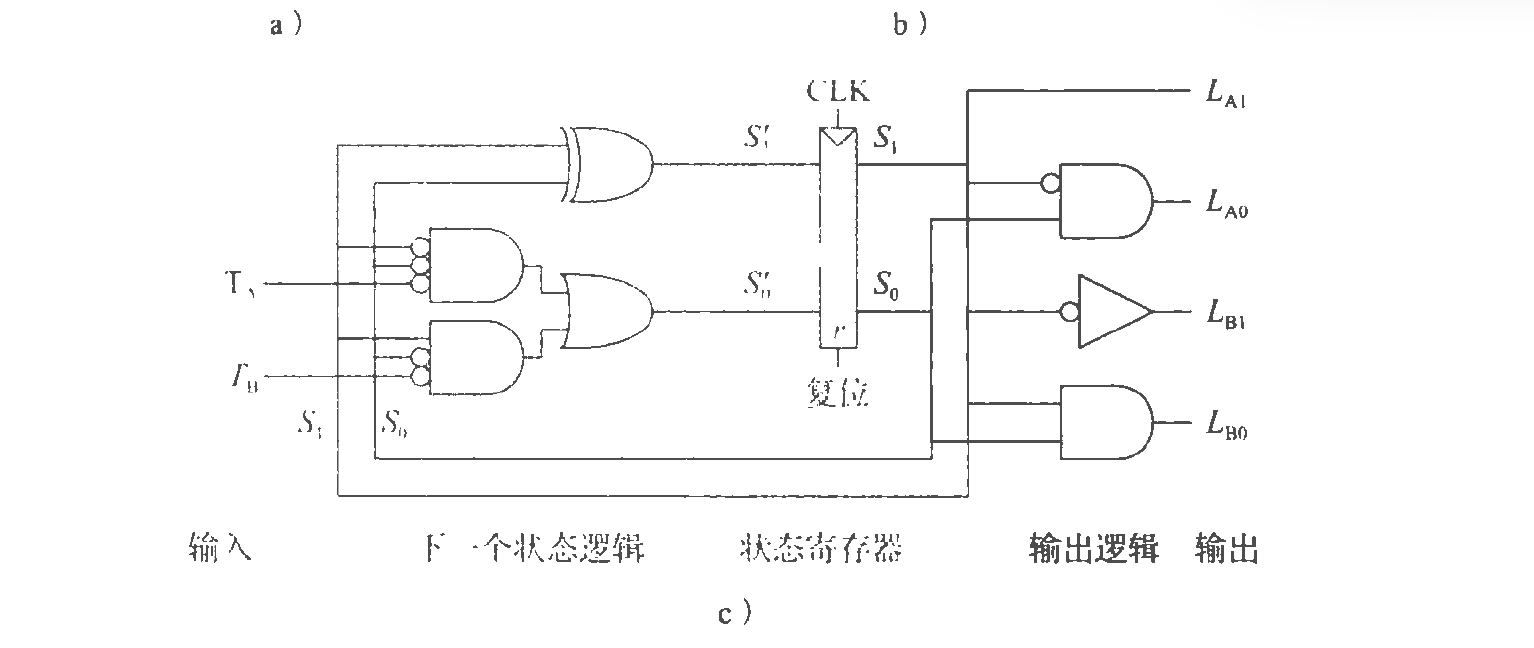
时序图如下:
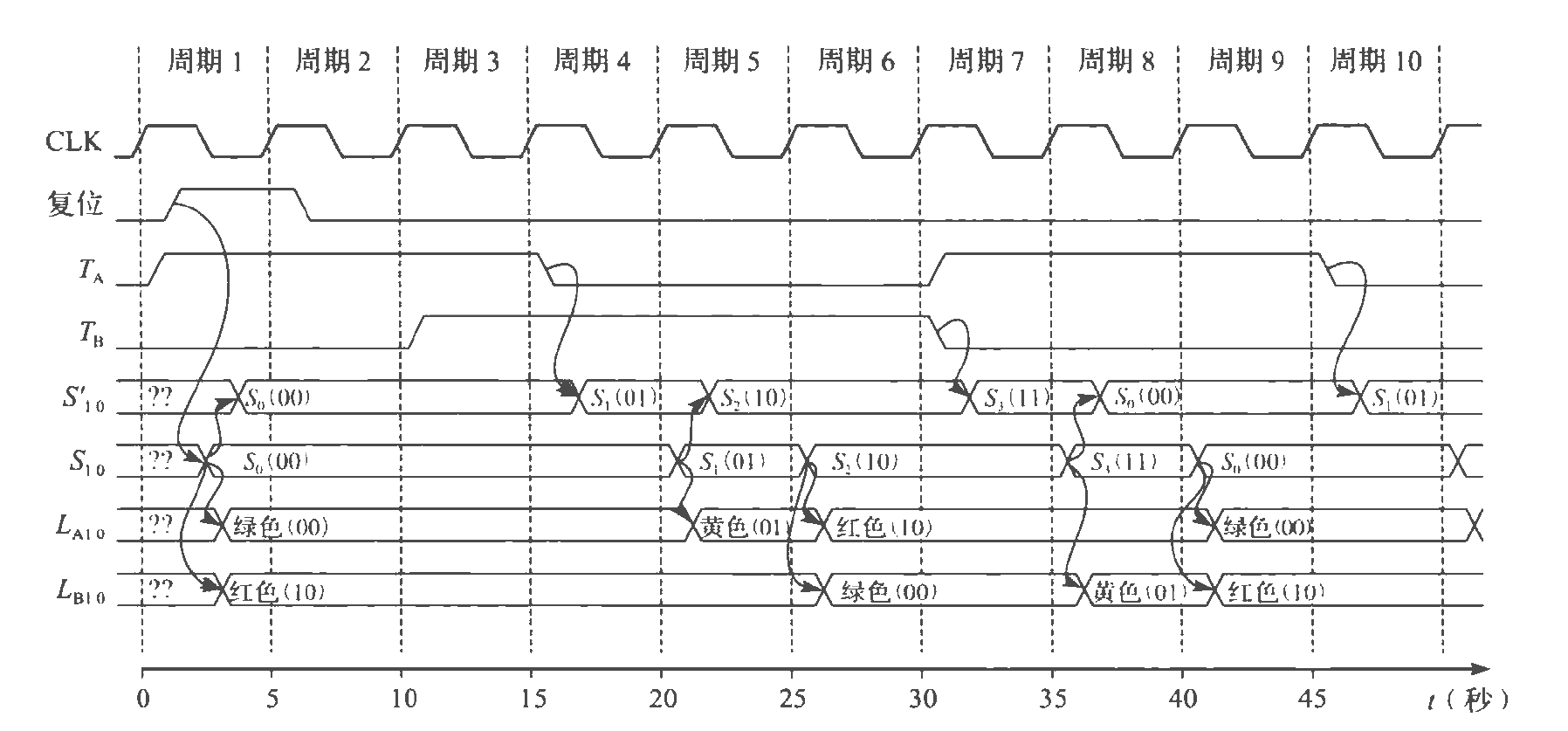
第一周期:
- 启动复位,升到高电平,延迟到$S_{1:0}$,然后延迟到其他门。
- $S_{1:0}$作为状态逻辑的参与部分,因变化延迟到$S_{1:0}^`$
- CLK每次位于上升期,$S_{1:0}$都会继承$S_{1:0}^
$,若$S_{1:0}^$无变化,则无延迟出现
第二周期:
- $T_A$保持为高电平,因此保持原状态。
第三周期:
- $T_A,T_B$都升高,但仍保持原状态
第四周期:
- $T_A$变换为低电平,进入下一阶段
第五周期:
- $S_{1:0}$作为输出延迟到状态改变,作为输入延迟到$S_{1:0}^`$
第六周期:
- $S_{1:0}$随时间变化,引起状态改变
……
例二
Alyssa P. Hacker有一个带限状态机大脑的宠物机器蜗牛。蜗牛沿着纸带从左向右爬行,这个纸带包含l和0的序列。在每一个时钟周期,蜗牛爬行到下一位。蜗牛从左到右在纸带上爬行,当最后经过的2位是01时,蜗牛会高兴得笑起来。设计一个有限状态机来计算蜗牛何时 会笑。输人A是蜗牛触角下面的位。当蜗牛笑时,输出Y为TURE。比较Moore型状态机和Mealy型状态机的设计。画出包含输入、状态和输出的每种机骈的时序图,蜗牛的爬行序列是0100110111。
此例较为复杂,需要考虑前置,现在和接下来的输入。
—————————————————-Moore(状态逻辑由当前状态和输入共同决定
由题意,开始序列为0,记为事件$S_0$(起始序列或循坏开始),此时还没有开始爬行。
若输入为0,认为开始了新状态,记$S_1$。反之,认为进行了01序列,停留在$S_0$.(起始为1毫无意义)
进入$s_1$,若输入为0,则需要等待1,停留。反之,凑齐条件,进入$S_2$,输出1。
进入状态$s_2$,若输入为0,转到$s_1$,等到1。反之,重新开始循环。
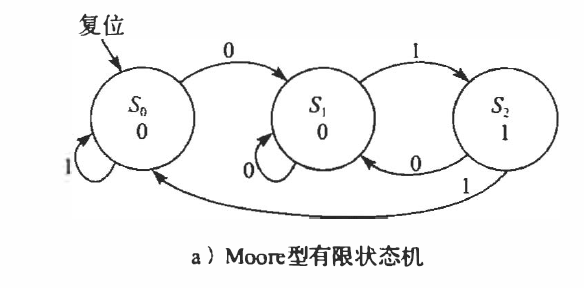
由此得到moore型状态机的状态转换图和输出表
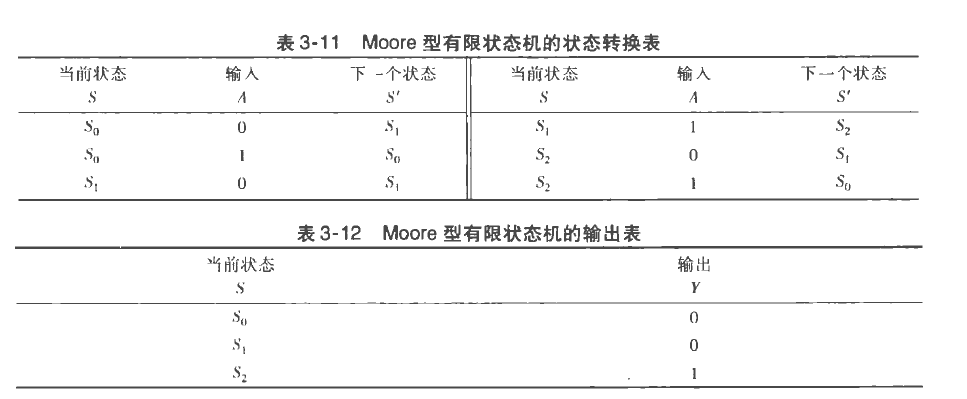
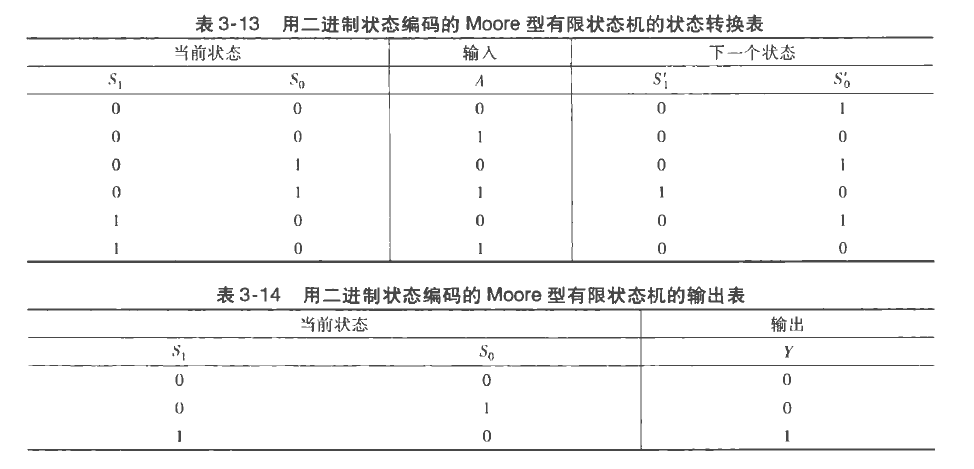
剩下的你肯定会。
————————————————mealy(输出逻辑由当前状态和输入共同决定)
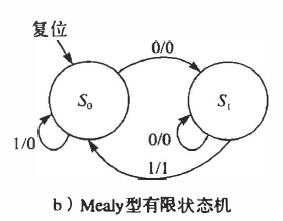
总体道理没差,只有输出被直接抛出,而不是通过状态的改变之后输出
状态编码
独热编码:对n种状态,有n个二进制位,每位1表示为这个状态,反之为其他。

只有1个1,表示启动哪个状态
二进制编码:对4个状态,只用2个二进制位,即$log_2 4$.
时序逻辑的时序
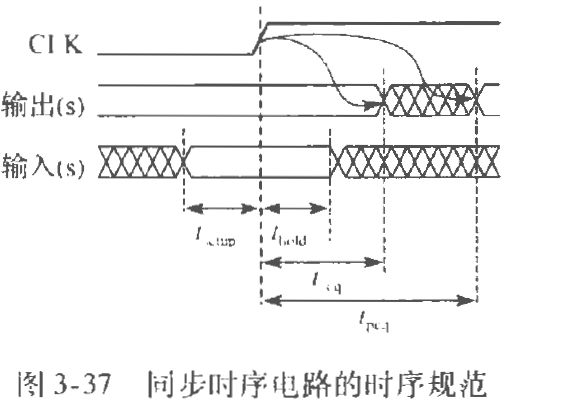
(图片有些糊
建立时间(set time),上升沿的前半段,$t_{setup}$。
保持时间(aperture time),上升沿的后半段,$t_{hold}$。
孔径时间=建立时间+保持时间,输入只有在孔径时间内保持稳定才能得到稳定的输出。
$t_{ccq}$,表示最小延迟,用于输出开始变化时间。
$t_{pcq}$表示传播延迟,用于输出保持稳定。
建立时间约束
两个寄存器间建立时间的约束,用于最长路
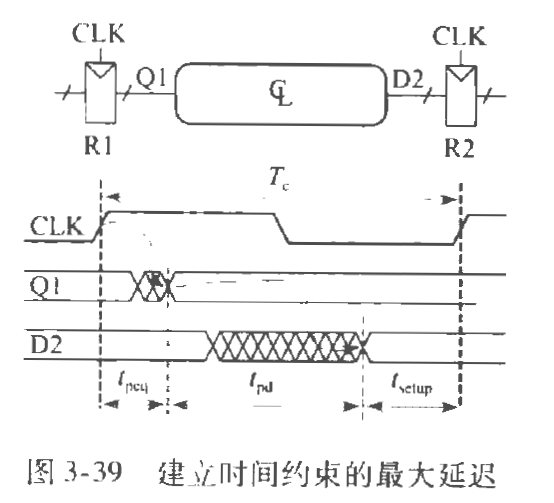
$t_{pd}$为门的最大延迟时间。
用于得到最小周期为$T_c$,(或最大频率),$T_c>=t_{pcq}+t_{pd}+t_{setup}$,
建立时间的要求
保持时间约束
两个寄存器间的保持时间的约束,用于最短路
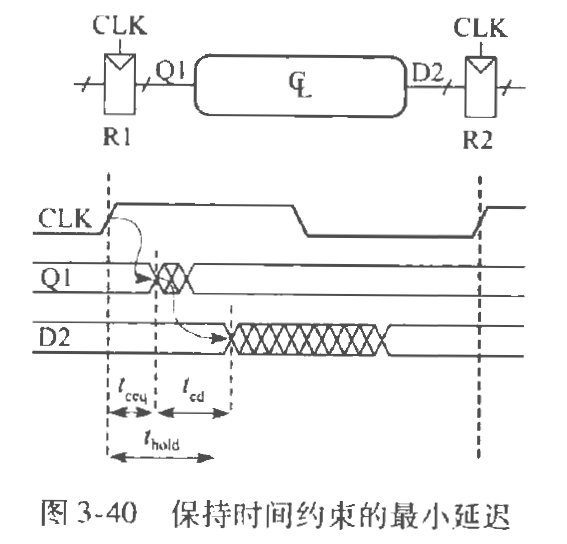
$t_{cd}$为门的最小延迟。
有$t_{ccq}+t_{cd}>=t_{hold}$,即寄存器规定的保持时间要小于寄存器的最小延迟与门的最小延迟之和
用于判断电路的时序是否合规,若不合规,则需要添加缓冲器使不等式成立。
同步器没讲
并行
任务(token)
延迟(latency)
吞吐量(throughput)
空间并行:增加设备,延迟不变,但吞吐量增加
时间并行:折叠任务,延迟不变,吞吐量增加
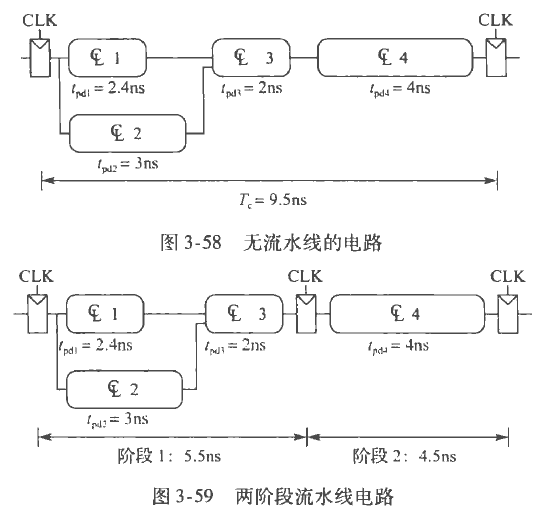
由上,增加寄存器后,最小周期:$9.5->5.5$
延迟:$9.5->11$
吞吐量:$1/9.5->1/5.5$
习题
1.根据波形图画出输出Q
(1)SR锁存器:需要一点点的延迟,1 1的无意义组合要归零,划线时还是以上升沿为主
(2)D锁存器:需要滞后,其余的看原理,简略点为clk为1时Q延迟与D对齐,为0时保持不变
(3)D触发器:需要滞后,只有在上升沿时需要看D形式。
2.区分时序和逻辑电路
时序电路:有寄存器,有回路,回路经过寄存器。
3.设置有限状态机
moore型:
注意输出由结果状态决定,即不需要输入参与构建输出的门
mealy型:
注意输出由结果状态和输入决定,二者共同参与构建输出门例:
mealy型、
Aly的蜗牛有一个女儿, 它有 个Mealy型状态机的有限状态机大脑 ,当蜗牛女儿爬过1101或1110时就会微笑。为这只快乐的蜗牛用尽可能少的状态画出状态转换图。 选择状态的编码, 使用你的编码写出组合的状态转换表和输出表。 写出下一个 状态和输出的等式, 画出有限状态机的原理图。
遇到此题,就应该开始构建状态转移图。
第一步应该会联想到此前做过的相似题,第一个状态应该设置为空输入状态,当输入1时才意味着进入了预设的1110或1101,反之就仍需要把状态置空,等待下一个1。需要注意的是,第一步都需要设置reset来复位,记得画复位。
第二步就为搭建剩余的状态,需要注意的是,在110和111处分开,此后的每个输入都会影响而产生新的状态,所以需要化简状态数量
注意到:
- 1110的后三位是1101的前三位,状态数减少
- 1111的后三位为1110的前三位,状态数减少
- 1101的后一位为11前缀的第一位,状态数减少
- 1100的后一位为0,回归空状态,状态数减少
由此,状态图大致成功,剩余的就只有补齐每个状态面对不同输入的所有情况即可
第三步,对mealy状态机,由于结果由输入和当前状态界定,下一状态由当前状态和输入决定,简单说就是时序,所以
得到部份表,与moore不同,moore在构建输出门户时只需要输出和当前状态的表,而mealy则由最小式综合考量
可以看到如上的表达式会比较精简,原因为表格中状态为110和111的部分可以全部设置为x,即不重要,加入表达式中就可以化简
电路图会有一些沟槽的化简,不必在意
moore型
就像逻辑电路,按部就班走,到了哪个状态就打哪个输出
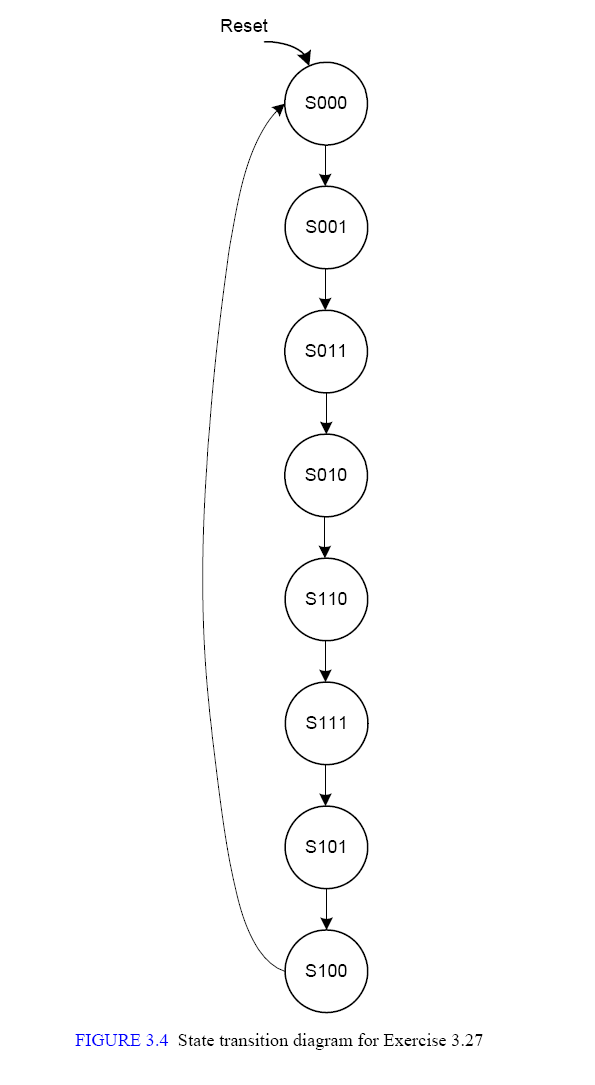
以格雷码转换为例,课本习题3.27
就是典型的moore型
不多说了
4.时序时间:
最小运行周期/最大运行频率$T_c>=t_{pcq}+t_{pd}+t_{setup}+t_{skew}$,
(1)锁定最长路,求出总的$t_{pd}$,其余两个带入即可
单位:$1 ps^{-1}=1*10^{-3}GHz$
保持时间约束
$t_{ccq}+t_{cd}>=t_{hold}+t_{skew}$
用于最短路
5.MTBF
硬件描绘语言
默认使用$System Verilog$
基础用法
- 元件的输入输出操作
module sillyfunction(input logic a,b,c, 元件的输入 |
- 多输入对应输出
module inv(input logic[3:0]a, |
- 一些门
module gates(input logic[3:0]a,b, |
- 缩减运算符
module and8(intput logic[7:0]a,output logic y); |
- 条件运算
module mux2(input logic[3:0]d0,d1, |
- 内部变量
module test(input logic a,b, |
- 优先级

- 数字
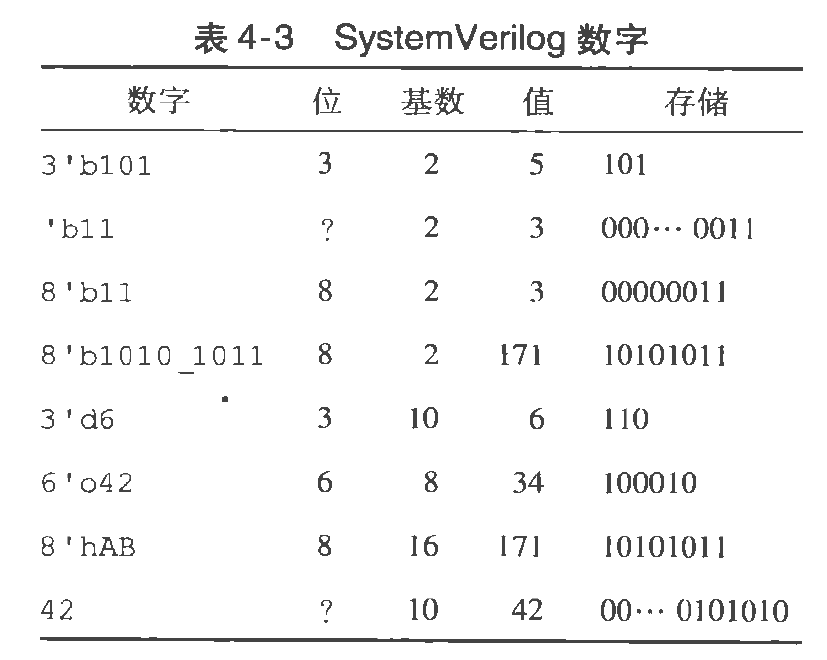
存在固定格式,共三块。 |
- Z和X
前情提要: |
module test(input logic a, |
- 常量
parameter green = 2'b00; |
- 位混合
module test(input logic [3:0]a,b, |
- 延迟
·timescale 1ns/1ps 表示时间单位 |
- 结构建模
module test(input logic a,b, |
always
- always_comb
在SystemVerilog中,always_comb块通常用于描述组合逻辑,即逻辑输出只依赖于当前输入的情况。然而,并非所有的组合逻辑都需要放在always_comb块中。有些情况下,组合逻辑的行为可能已经被其他语言结构明确地描述了,而不需要always_comb块。 |
时序逻辑
- 寄存器
module test(input logic clk, |
<=为非阻塞赋值,用于时序电路 |
- 带复位功能的寄存器
异步复位器 |
同步复位器 |
always_ff 表示在时钟的上升沿触发。 |
- 带使能端的寄存器
异步使能复位寄存器 |
- 同步器
module test(input logic clk, |
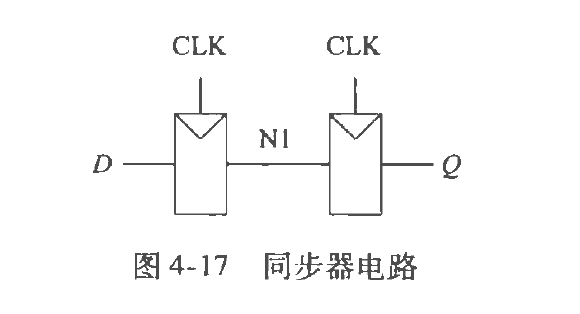
如图,n1作为中间变量,写在CLk下面,天然就是一个寄存器。 |
- 锁存器
module test(input logic clk, |
always_lanth相当于always@(clk,d),是专门用来修饰锁存器的 |
组合电路
- 使用always的组合反相器
作为组合电路,应使用=(阻塞赋值 |
- 全加器
module inv(input logic a,b,cin, |
- 七段管显示译码器
module inv(input logic [3:0] data, |
case必须在always语句内 |
- 使用无关项的优先级电路
module inv(input logic [3:0] a, |
casez可以识别无关项 |
- 优先级电路
module inv(input logic [3:0] a, |
阻塞与非阻塞
- 对<=来说,在一个always内,所有的非阻塞同时计算,这意味在参与计算的值若也是非阻塞,那么参与计算的是原值,而非计算后的值。——-即考虑前一个状态
- 对=来说,在一个always内,按照代码顺序依次计算。
有限状态机
module test(input logic clk, |
习题:
主要考察普通设计时的语法注意事项以及always用法和状态机的设计
普通设计:
- 需要区分译码器,复用器以及优先电路
译码器为将n个输出组合为$2^n$个状态,通过输出的01组合得到电路
未组合的版本如下(2:4)
case(input)
2`b00: y=4`b0001
2`b01: y=4`b0010
2`b10: y=4`b0100
2`b11: y=4`b1000
endcase复用器为通过输入选择让哪个输入进入
如下
case(input)
2`b00: y=i1
2`b01: y=i2
2`b10: y=i3
2`b11: y=i4
endcase优先电路为只看最前位的输入,得到其位置或编码
如下
case(input)
4`b1???:y=4`b1000
4`b01??: y=4`b0100
4`b001?: y=4`b0010
4`b0001: y=4`b0001
4`b0000: y=4`b0000
- 需要注意使用case()要使用always_comb
需要注意case的语法
case(input)
2`b00:...
2`b01:begin ... end
default : ...
endcase
- 需要注意优先状态机的格式
moore
input logic c,
output logic p)
typedef enum logic [1:0] {s0=2`b00,s1,s2} statetype;
//此处为枚举,[1:0]由你的状态数决定,每个状态可以单独赋值,这是为特殊的编码机制,如格雷译码器准备的
statetype [1:0] state,nextstate;
//创建两个枚举
always_ff @(posedge,clk,posedge reset)
if(reset) state<=s0;//此处为时钟上升沿所要进行的操作,需要使用非阻塞式的赋值
else state<=nextstate;//此处表示未进行复位,模拟继续
always_comb
case(state)
s0: if()nextstate=s1;
else nextstate=s0;
s1: if()nextstate=s2;
else nextstate=s0;
s2: nextstate=s0;
default: nextstate=s0;
endcase//表示状态的转移
assign y=state[?]|state[?]//此处表示输出y的布尔表达式
mealy
input logic c,
output logic p)
typedef enum logic [1:0] {s0=2`b00,s1,s2} statetype;
statetype [1:0] state,nextstate;
always_ff @(posedge,clk,posedge reset)
if(reset) state<=s0;
else state<=nextstate;
always_comb
case(state)
s0: if()nextstate=s1;
else nextstate=s0;
s1: if()nextstate=s2;
else nextstate=s0;
s2: nextstate=s0;
default nextstate=s0;
endcase//表示状态的转移
always_comb
case(state)
s0: if() q=?;
else q=?;
s1: if() q=?;
else q=?;
s2: q=?;
default q=?;
endcase
//这一步可以根据状态转移图理解
endmodule
- 其他
always_comb可以理解为一个大型的assign,其中不需要<=,不要求一定包含case
- 需要注意其他电路的代码实现
数字模块
算数电路
加法
半加器
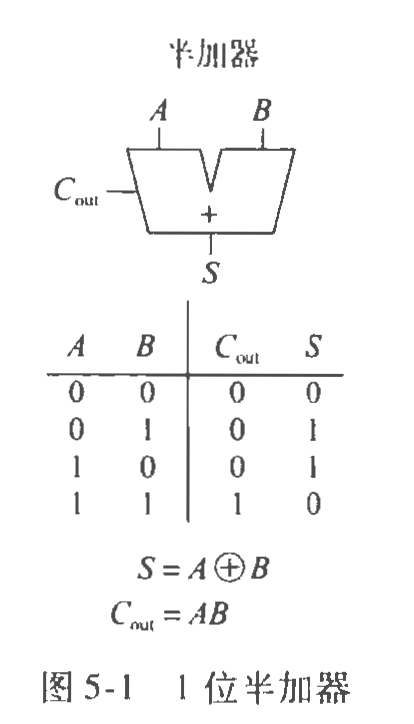
两个输入A,B得到两个输出S,$C_{out}$。其中两个输出代表了A,B的和,C_{out}表示进位,S表示去除进位后的值。例如1+1=2,进位1,C_{out}=1,S=0
全加器
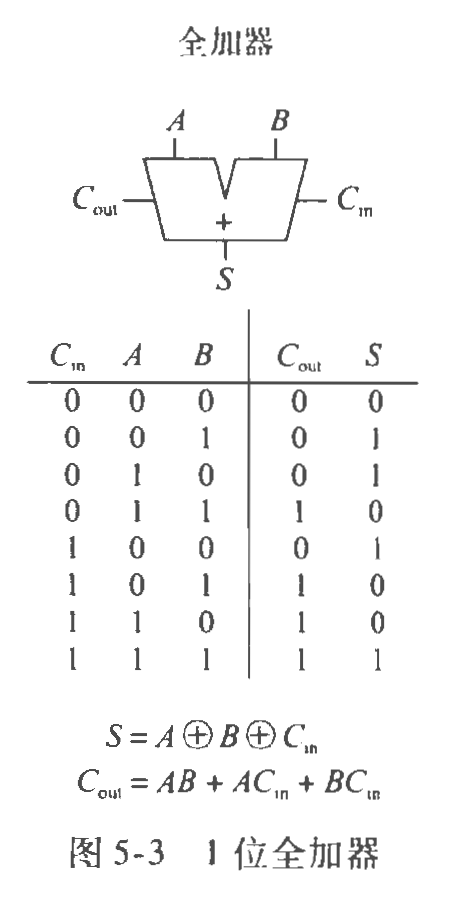
全加器利用了输出C_{out},它接收一个进位输入,利用这个进位信息再向上一级生成进位。例如11+11,此时从末尾进一,首位向前进一,得到100;
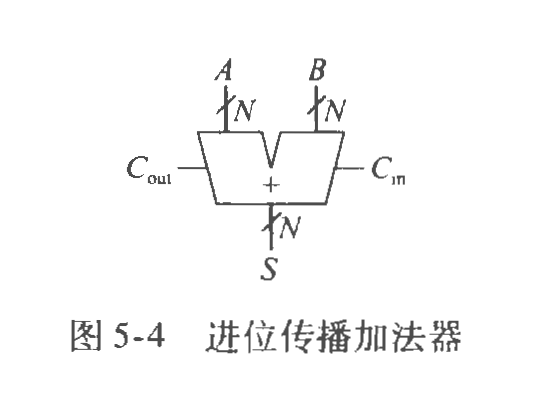
进位传播加法器(CPA)
行波进位加法器
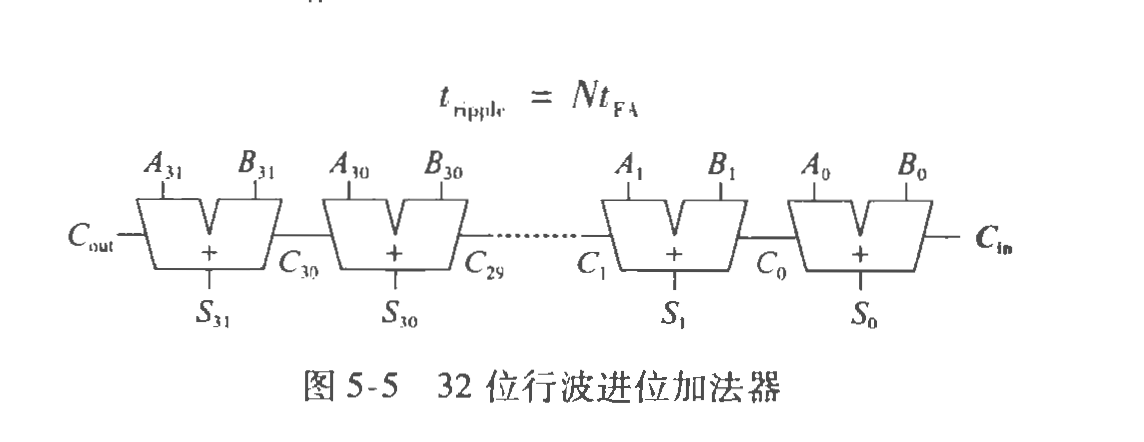
结果需要前一位的进一,依次累加,即进位通过进位链形成行波。$t_{ripper}$是单个加法器的延迟,而$t_{FA}$是全体加法器时间的累加。有关系:
先行进位加法器(CLA)
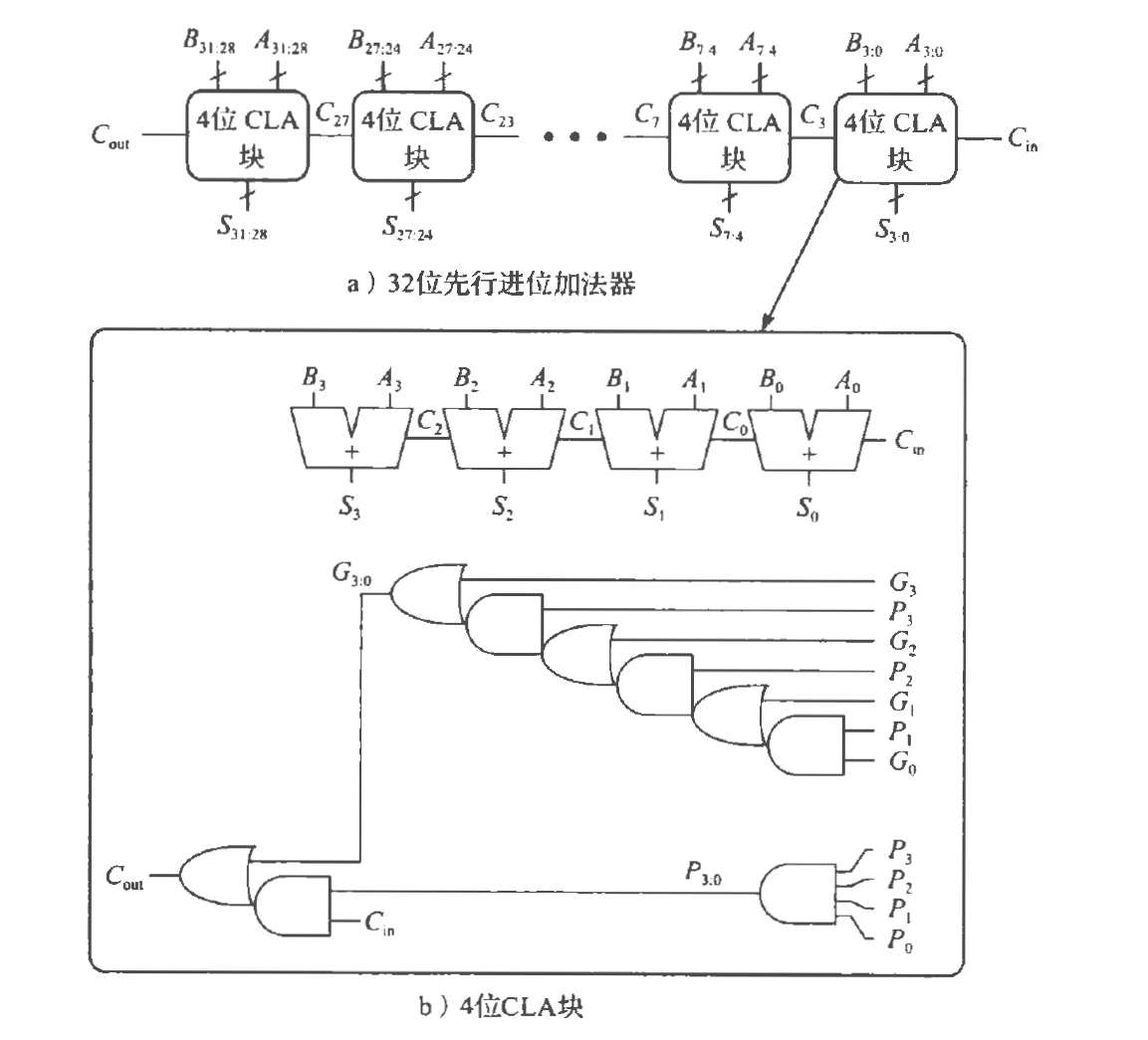
先分块,再产生输出。
对每个分块,都有接收一个进位输入,产生一个进位输出。
对于进位输出,需要块的两个性质:产生进位和传播进位。
产生进位
这是块自己得到进位输出的能力,例如1+1就会自动产生进位。记为$G_i$,i为序号
传播进位
这是块根据进位输入得到进位输出的能力,例如1+0和进位1就会输出一个进位1。记为$P_i$,i为序号
进位输出
依照这个公式,可以得到各级的进位输出
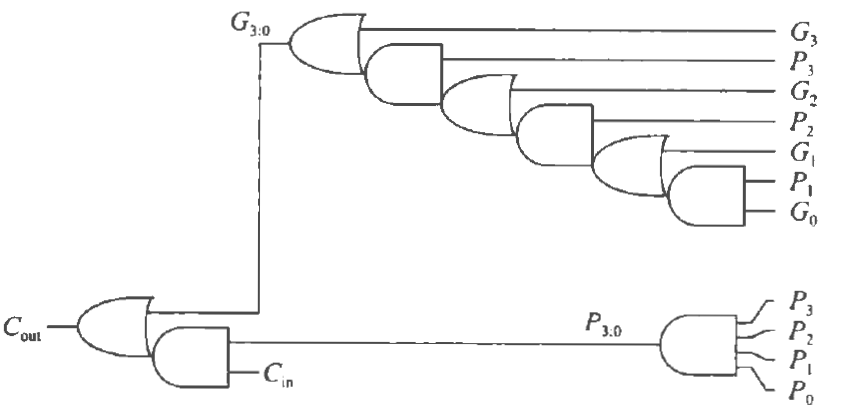
依照该图,右上侧得到四位的产生进位G,右下角为传播进位P,根据进位输入$C_{in}$得到块的进位输出$C_{out}$
时间延迟
其中$t_{pg}$为产生$p_i$, 和$G_i$的单个产生/传播门(单个AND或OR门)的延迟,$t_{pgblock}$为在K位块中寻找产生信号$P_{ij}$和传播信号$G_{ij}$的延迟,$t_{AND-OR}$为从$C_{in}$到$C_{out}$到达K位CLA块的最后AND/OR逻辑的延迟。
事实上,从最长路来看,
- 每个块都同时开算,有$(2*(k-1))$个门的延迟和4个全加器的延迟;
- 后方的块停留在$C_{In}$,因此结果需要加上这些余下块的两个门的延迟;
- 从第一块开始,由最长路,有$(2*(k-1))+1$个门
- 合在一起四部分
加法器
module test #(parameter n=8) |
input logic [n-1:0] a, b:这是两个 n 位的输入端口 a 和 b,用于存放待相加的数。 |
减法
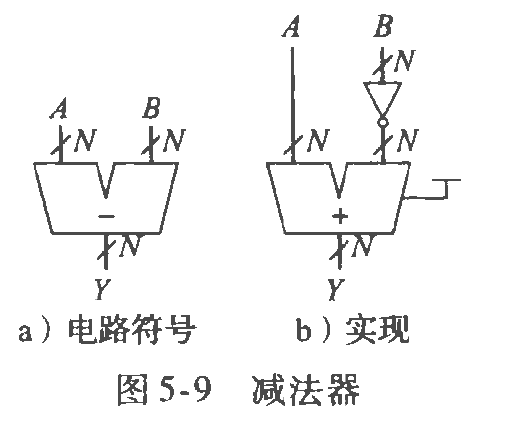
这是第一章的复现,将二进制负值转换为补码。
B输入处的取反就是取补码,这通常还需要加一,即一个初始值为1的进位输入(作用到第一位)。
module subtractor #(parameter N -8) |
你一定会 |
比较器
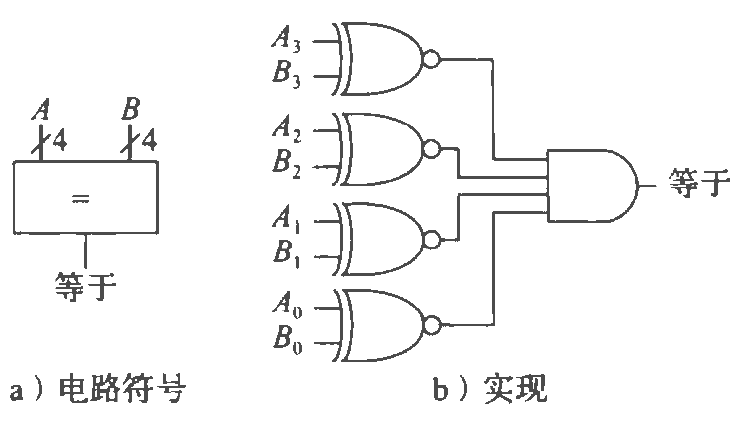
比较简单,你一定会
module comparator #(parameter N =8) |
算数逻辑单元

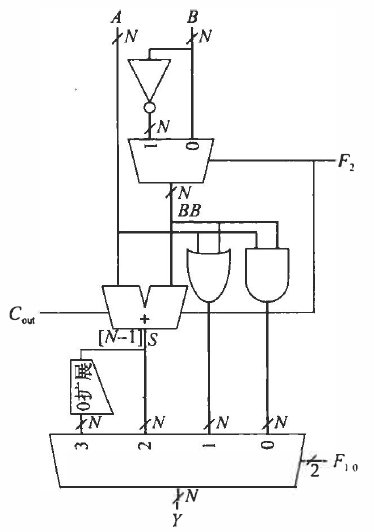
根据图一的运算编码,得到F[2:0],第一位F2作为判断B是否取补,剩下的两位判断模式,根据复用器使对应的输出通道打开。F2还作为加法器的初始进位输入,对于无符号加法,进位输入为0,反之需要补码时,进位自然为1(因为补码本身需要加1),011安装了扩展,用来扩展位数。
移位器和循环移位器
逻辑移位器
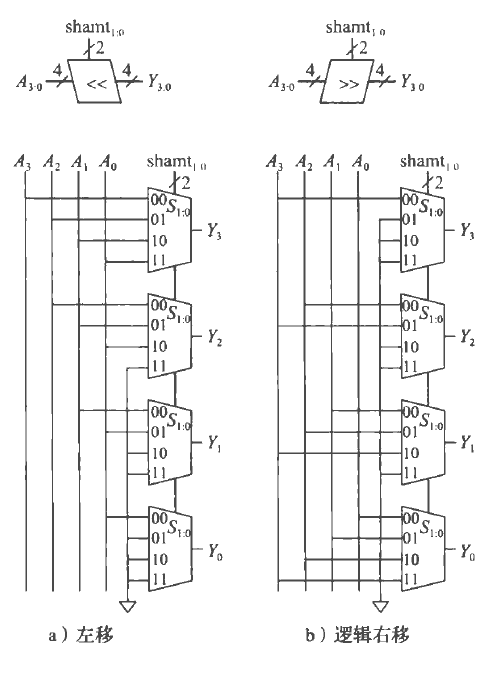
就像是枚举,shamt选择模式,00表示左/右移动0位,01表示1位,,,
算数移位器
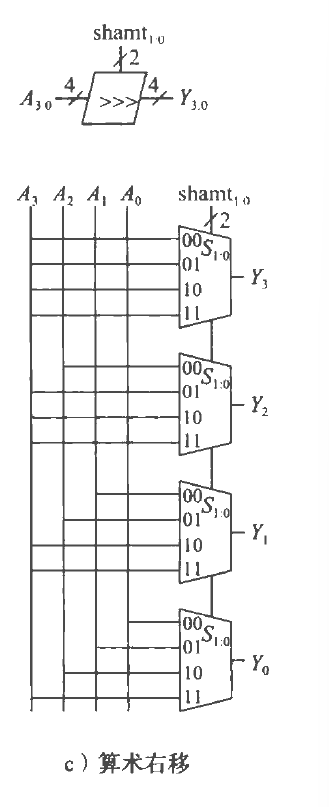
基本原理一致,但多了一个规则,原数据的最高有效位会继承到被右移的那位。
如图11000->11100->11110->11111为累次移动一位的过程。
即a3a2a1a0->a3a3a2a1->a3a3a3a2->a3a3a3a3
乘法(*?)
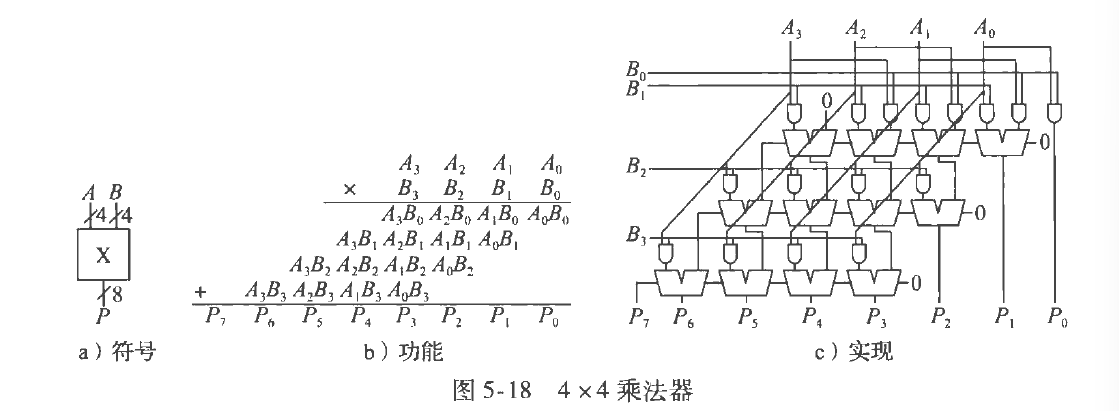
和十进制乘法一样,小学的玩意。即加法的累加
除法(*?)
大概不考。
数制
定点数
是你学过的二进制小数点算法。

看个样例乐呵下,补码加一在小数末尾;建议使用原文的思路
时序电路模块
计数器

时钟打一次,就把1在加法器中的结果打出去,既输出,又作为下一次的加数。
module counter #(parameter N=8) |
移位寄存器

上图所示为串行到并行的移位寄存器。时钟每打一次,$S_m$的值就会被输出记录,且已经被记录的会在输出中前进一位,这样n个周期后,就能并行访问所有的$S_m$(即[N-1:0]个输出)
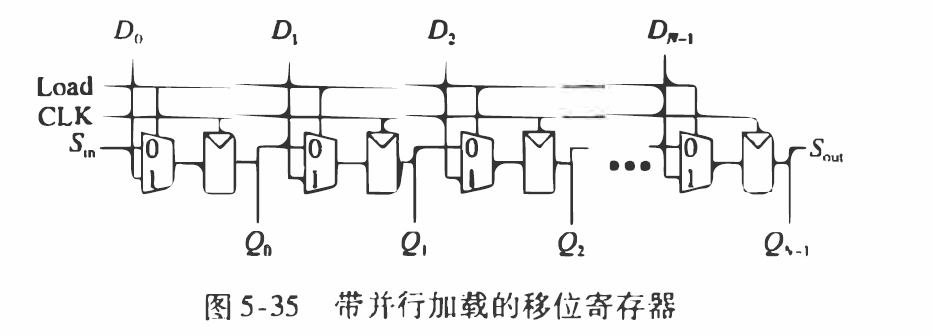
上图为可切换的并行移位器,使能信号Load为1时,由l[N-1:0]并行输入,同时可以并行访问。为0时和上面的一样。这样就能使并行的输入被一次次移位。
module shiftreg #(parameter N=8) |
input logic clk:时钟输入端口,用于控制寄存器的时钟。 |
存储器阵列
基础
动态随机访问存储器
静态随机访问存储器
只读存储器
地址
数据
深度
宽度
阵列
位线
字线
阵列的单位为位单元,每个位单元都被一个位线和一个字线连接
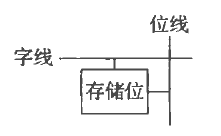
字线是高电平时用来启动这个位单元,这时位线连接到位单元用来读取或写入数据。
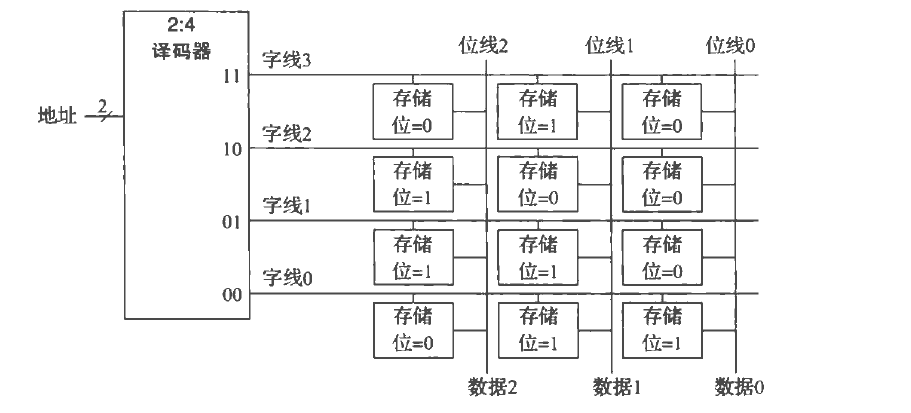
地址实际上就是字线的代码,读写以整个字为单位,读取时位线被设置成浮空,写入时位线被设置为要输入的值。
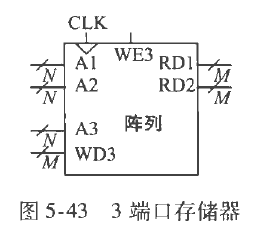
三端口存储器,A1,A2为读取端,A3为写入端。使能WE3无效时,从A1或A2读取数据放到RD1,RD2,有效时把WD3的内容写入A3
动态随机访问存储器
作为RAM的动态分支,它与SRAM一样是易失的。
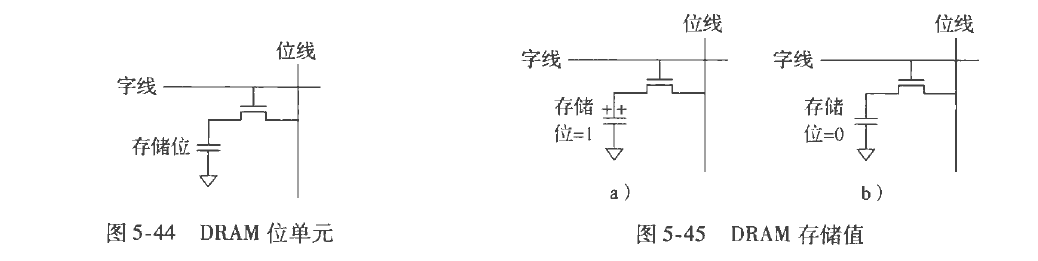
以电平的方式存储位,所以存储的内容会因电压的流失而流失,所以叫做动态,其内容需要快速的跟新。
读取时,数据从电平发送到位线,此时电平中不存在数据,所以需要重写数据;写入时数据从位线发送到电平。
静态随机访问存储器
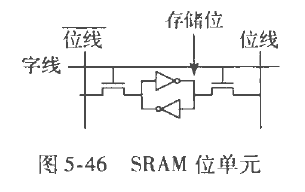
看到这个反相器应该就明白了,这个元件能存储数据,能满足写入读取
面积和延迟

寄存器文件
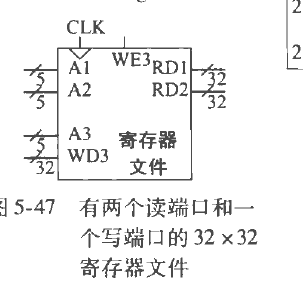
如上的三端口存储器,内部由SRAM组成
ROM
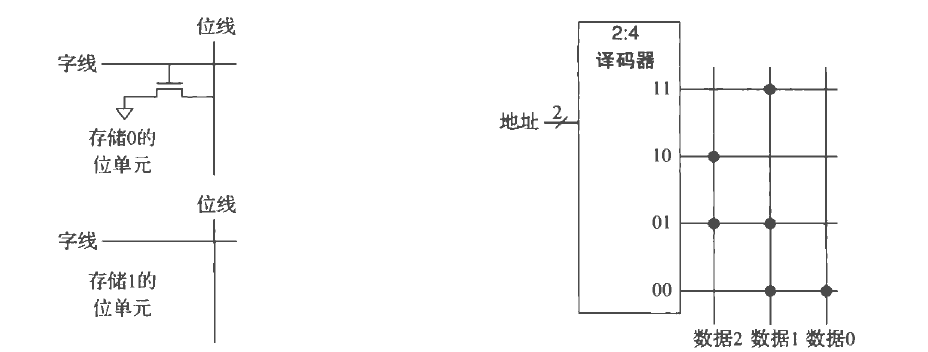
可以用晶体管的有无来判断存储的信息,有为0,反之为1,扣掉晶体管确实就只能只读了,但其他的长期存储不会只读。
右图上,有实点表示为1,否则为0
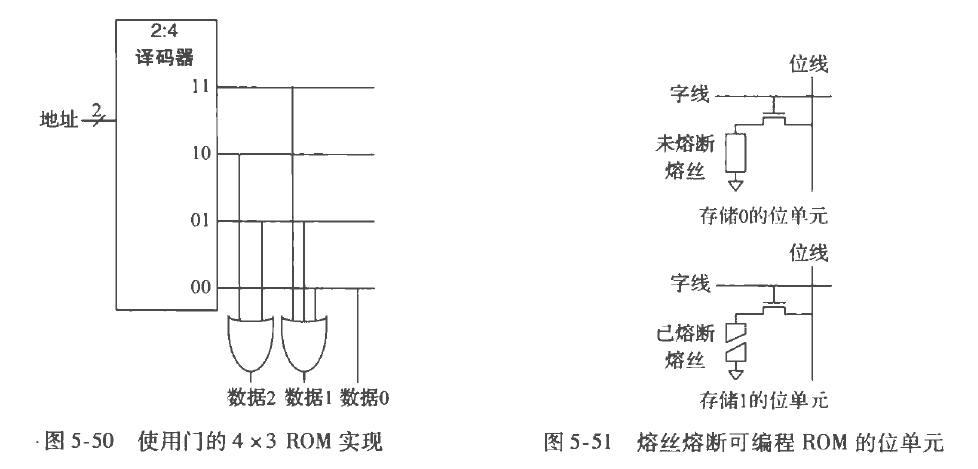
可得到对应的表达式
右图为一次性ROM,熔断熔丝后如果接地为0,否则为1.
使用存储器阵列的逻辑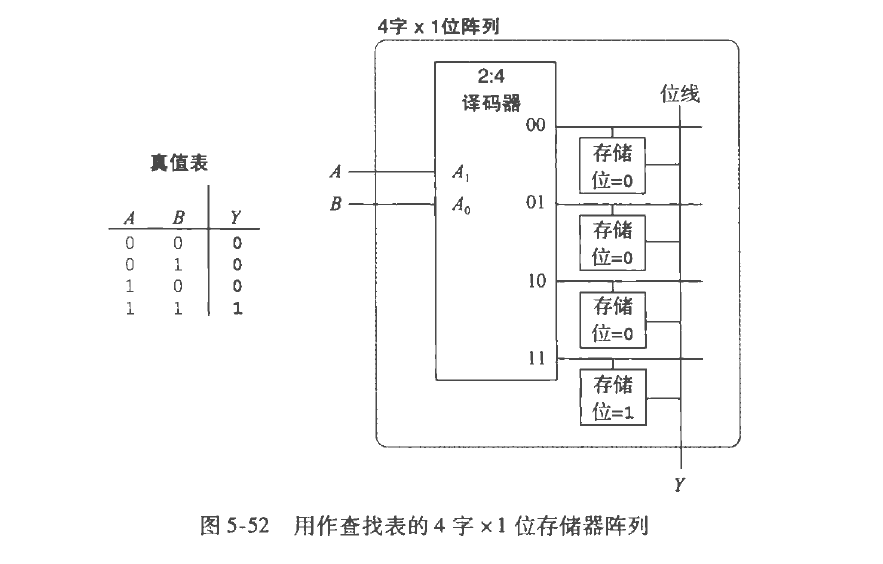
实质为将每个数据转化为一个逻辑而非晶体管
存储器代码
RAM
module ram#(parameter N=6,M=32) |
clk:时钟信号,类型为logic。 |
ROM
module rom(input logic [1:0] adr, |
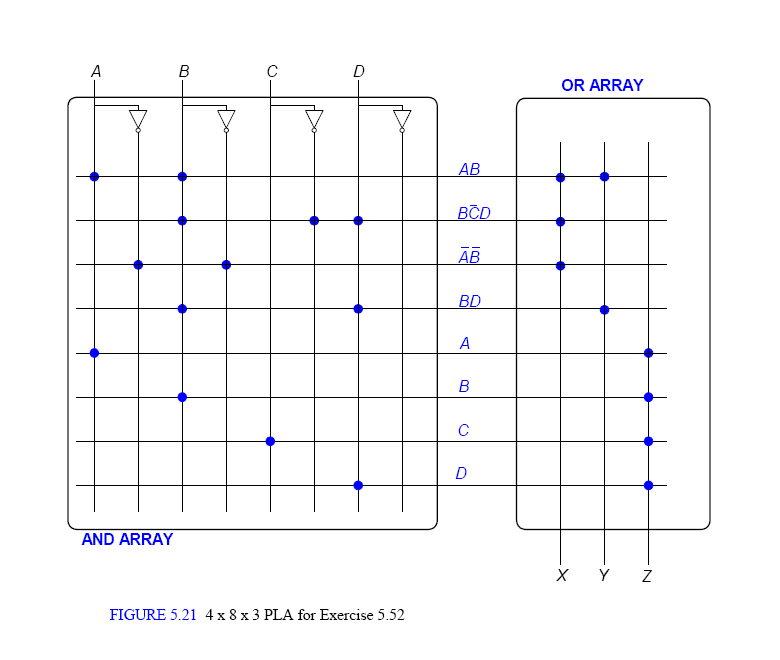
可编程逻辑阵列
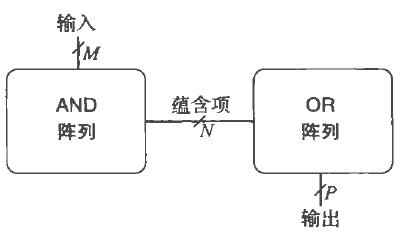
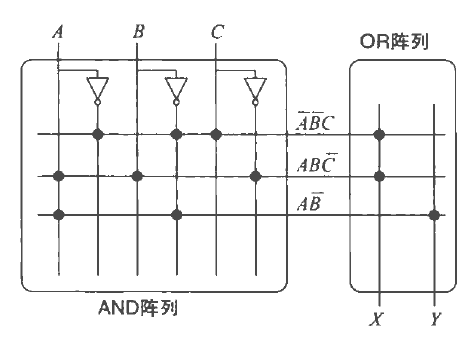
顾名思义AND阵,根据实点取值,在OR阵列中取和。
未勾点的不会进入,可视为浮空。
习题
1.计算延迟
对于行波进位加法器,n位加法器有b个全加器,时间延迟为n个全加器延迟之和
对于先行进位加法器,需要理解其所有块的计算同时开始,需要等待的只有每一位的$C_{out}$,因此时间延迟为第一个块中全加器的总延迟+第一个块中得到$C_{out}$的OR/AND门数量(4位就有6个)+第一个块中的输出OR+剩余其他块各自所需的2*AND/OR时间延迟
- 考察各种电路原理图
- 定点二进制数的转换
(1)十进制转二进制
(2)二进制转补码(小数位加1)
(3)二进制转16进制(0x….,不计小数位,从右往左一次4位)(0b表示二进制,0o表示8进制,十进制不做特殊标识,0x表示16进制,均可大写)
4.ROM实现布尔表达式
给出式子带入值,实点为1,反之为0
- PLA实现布尔表达式
根据需求勾选