数据结构
前情提要
算数
指数,对数,级数,模运算
证明方法
递归简论
c++
算法分析
时间复杂度

依次为小于等于,大于等于,等于,小于
部分公式
一般的,计算复杂度即为计算最内层循环的次数,需要等差和等比的前n项和。
空间复杂度
表,栈和队列
抽象数据类型(ADT)
能够实现类似于删除,插入,修改,搜索,比较等操作的数据结构,不同于整数,实数等的数据结构
表(List)
也称顺序存储(sequential)
List的数组实现
有四个主要的数据成员:存储长度,最大长度,数组,当前指针
有两个主要函数:插入(curr前插入),删除(curr节点删除并返回)
using namespace std;
template<class T>
class List{
private:
//存储数据的数组
vector<T> data;
//帮提供给用户的指针
//接下来所有的操作都要依赖此指针
int curr;
//逻辑上的大小
int listSize;
//实际上为应对扩容而实现的大小
int maxSize;
public:
//用最值创建列表
List(int max=120):maxSize(max+10),listSize(max)
{
data.resize(max+10);
//按最大内容分配,当然用户能使用的只有ListSize
curr=0;
}
//主要函数1
void insert(int num)
//在curr前插入
{
if(listSize>=maxSize)
//若已满,则扩容
{
resize(maxSize+10);
maxSize+=10;
}
//从0开始,故以listSize起手
for(int i=listSize;i>curr;i--)
{
data[i]=data[i-1];
}
data[curr]=num;
//插入一位,故只加一
listSize++;
}
//主要函数2
T remove()
{
if(curr==listSize)
{
int empt=curr;
curr--;
listSize--;
return data[empt];
}
int empt2=data[curr];
for(int i=curr+1;curr<=listSize;i++)
{
data[i-1]=data[i];
}
listSize--;
return empt2;
}
bool move(int pos)
{
if(pos<0||pos>=listSize)
{
return false;
}
else
{
curr=pos;
return true;
}
}
void resize(int n)
{
data.resize(n+10);
}
void moveToStart()
{
curr=0;
}
void moveToEnd()
{
curr=listSize;
}
void prev()
{
if(curr>0)
curr--;
}
void next()
{
if(curr<listSize)
curr++;
}
int length()
{
return listSize;
}
int currPos()
{
return curr;
}
int getValue()
{
return data[curr];
}
void setValue(int num)
{
data[curr]=num;
}
void clear()
{
maxSize=0;
listSize=0;
resize(0);
}
};
int main(){
}
List的链表实现
单向链表
链(next link)
有四个主要的数据成员:头指针,尾指针,当前指针。不需要数组,一切插入都基于这三个指针。
有两个主要函数:链表节点的构造(用于插入算法),插入(curr后插入),删除(curr后节点删除并返回值)
|
双向链表
无官方代码,凑合看一下
|
比较数组实现和链表实现:
$n(P+E)$表示链表实现的空间占用,n是总的节点数,P是指针空间大小,E是数据空间大小
$EN$表示数组实现的空间占用,N是数组的元素数目,E是数据空间大小
值更小的更优
迭代器
1.本身是可迭代的、
2.本身可以访问到下一个元素(指针)
迭代器是STL中数据结构的单位
常量容器和非常量容器使用诸如begin(),end()方法时返回的迭代器不同,分别为const_iterator和iterator
vector的实现
稍看几眼即可{} 也可以用于初始化容器类型或其他支持初始化列表的类型。例如,你可以用 {} 来初始化一个 std::vector<int> 对象
using namespace std;
template <class object>
class Vector
{
public:
Vector(int size=0 ):thisSize(size),theCapacity(size+spare)
{
node=new object[theCapacity];
}
Vector(const Vector& rhs):theSize(rhs.theSize),theCapacity(rhs.theCapacity),node(nullptr)
{
node=new object[theCapacity];
for(int i=0;i!=thesize;++i)
{
node[i]=rhs.node[i];
}
}
Vector &operator= (const Vector& rhs)
{
Vector empt=rhs;
swap(*this,empt);
return *this;
}
~Vector ()
{
delete [] node;
}
Vector(Vector &&rhs):theSize(rhs.theSize),theCapacity(rhs.theCapacity),node(rhs.node)
{
rhs.node=nullptr;
rhs.theSize=0;
rhs.theCapacity=0;
}
Vector & operator=(Vector && rhs)
{
swap(*this,rhs);
swap(theSize,rhs.theSize);
swap(theCapacity,rhs.theCapacity);
return *this;
}
void resize(int newSize)
{
if(newSize>theCapacity)
{
reserver(newSize);
}
theSize=newSize;
}
void reserve(int newCapacity)
{
if(newCapacity<theSize)
{
return;
}
object *newArry=new object[newCapacity];
for(int i=0;i<theSize;++i)
{
newArry[i]=node[i];
}
theCapacity=newCapacity;
swao(node,newArry)
delete [] newArry;
}
object &operate[](int index)
{
return node[index];
}
const object& operator[](int index)const
{
return node[inex];
}
bool empty()const{
return size()==0;
}
int size()const
{
return theSize;
}
int capacity()const{
return theCapacity;
}
void push_back(const object &node)
{
if(theSize==theCapacity)
{
reserve(2*theCapacity+1);
}
node[theSize++]=x;
}
void push_back(onject && x)
{
if(theSize==theCapacity)
{
reserve(2*theCapacity+1);
}
node[theSize++]=std::move(x);
}
void pop_back()
{
theSizs--;
}
const object& back()const{
return node[theSize-1];
}
typedef object* iterator;
typedef const object* const_iterator;
iterator begin()
{
return &node[0];
}
const_iterator begin()const{
return &node[0];
}
iterator end()
{
return &node[theSize];
}
const_iterator end()
{
return &node[theSize];
}
static const int spare=16;
private:
object *node;
int theSize;
int theCapacity;
};
栈ADT
栈本身的三个重要函数:push,pop,topValue
栈的链表实现
重要函数为:push(单向链表,插入方向与指针方向相反),pop(弹出方向和指针方向相同)
|
栈(stack)的数组实现
有三个重要的数据成员:maxSize(因为不考虑扩充数组),top(定位),一个数组
使用vector的pop,push等实现
|
中序遍历的实现(栈)
队列(queue)
队列的数组实现(循环队列(loop circule))
考虑到普通队列使用数组实现会导致空间的大量浪费,故使用循环队列
事实上,以数组实现的队列满与空要看初始条件,在下面的例子中,由于空间多加了1位,所以初始条件位rear=0,front=1,此时队列自然为空(差值为1),队列是否为空也要靠这个判断。若差值为2,则自然为满。这种情况下,花费了两个空间标识了头与尾节点
若初始条件不会扩充空间,那么设置rear=0,front=0;差值为0,队列为空,差值为1,队列为满。这种情况下,花费了一个空间标识了头与尾节点,一般的,实践中更习惯这种用法
重要函数为:enqueue(注意取模和越界判断)和dequeue(取模)
using namespace std;
template <class E>
class Queue
{
private:
void operator=(const Queeue&){};
Queue(const Queue&){};
public:
Queue(){};
virtual ~Queue()=0;
virtual void clear()=0;
virtual void enqueue(const E& x)=0;
virtual E dequeue()=0;
virtual const E& frontValue()const=0;
virtual int length()const=0;
};
template <class E>
class AQueue:public Queue<E>
{
private:
int maxSize;
int front;
int rear;
E* array;
//int currSize;可用于检测是否溢出
public:
AQueue(int size=10)//default
{
maxSize=size+1;
rear=0;
front=1;
listArry=new E[maxSize];
}
~AQueue()
{
delete []listArry;
}
void clear()
{
rear=0;
front=1;
}
void enqueue(constE& item)
{
if((rear+2)%maxSize!=front)
{
rear=(rear+1)%maxSize;//比设定值大一
listArry[rear]=item;
}
}//先增后写入
E dequeue()
{
E item=listArry[front];
front=(front+1)%maxSize;
return item;
}
const E& frontValue()const{
return listArry[front];
}
virtual int length()const{
return (rear+maxSize-front)%maxSize;
}
};
队列的链表实现(非循环队列)
重要函数为:enqueue(顺着指针方向),dequeue(顺着指针方向)
//不考虑使用循环列表 |
树
根:无父
节点:
树叶:有父无子
兄弟:有相同父亲
路径:两节点间的线段数量
深度(depth):根到该节点的线段数,即深度是从0
高(height):该点到最远的叶节点
真祖先—真后裔:父子不相等
树的实现
考虑到为每个节点设置超出实际范围的指针数不灵活,改为为每个节点设置指向下一个兄弟和自己的儿子的指针。
using namespace std;
template <class object>
struct treeNode
{
object data;
treeNode* brother;
treeNode* child;
};
树的遍历
先序遍历(preorder):
根—左子树—-右子树`
中序遍历(inorder):
左子树—根—-右子树
一般通过表达式构建中序遍历树,再以此得到其他遍历
后续遍历(postorder):
左子树—右子树—-根
遍历实现
void preorder(treeNode* Tree) |
通过遍历得到的图的结果可能不唯一,但若有一个树的两个遍历时,那么就可以得到唯一的结果
-此处应链接一已知前序和中序求原树的代码
二叉树(Binary tree)
每个节点的儿子数不多于2
二叉查找树
左子树的所有值小于根,右子树的所有值大于根
表达式树
叶为操作数,节点为操作符。以三种不同的遍历方式能得到三种不同的表达式
即从先序等三种遍历的结果回溯到原本的树
二叉查找树
关键的函数有:contains(用bool反馈是否存在),findmin,insert(有点巧妙),delete(区别三种情况,无子,单子,)
指针的引用与普通指针的区别在于你想修改的是指针指向的地址的数据还是指针副本的数据,即指针副本的指向关系不会同步到本体上,但引用会
实现
|
AVL(注)
是二叉搜索树的衍生,但就平衡问题展开旋转操作
旋转
单旋
void rotateWithLeftChild(AvlNode*& t)//左左的单旋转,即单旋中的右旋 |
双旋
void doubleWithLeftChild(AvlNode*& t)//双旋中的右旋,只使用于目标节点左孩子的左孩子为空 |
AVL树的旋转,归结为:
自从下往上第一个不平衡的节点起,向下按顺序寻找两个节点(若这两个节点的形状机符合单旋转,又符合双旋转,则取单旋转),将这三个节点排序,原来的不平衡节点的父节点放置在先已经排序的根节点上,其余的子节点按原旋转方法放置。
高度
int height(AvlNode* t)const |
插入
void insert(const E& x,AvlNode*&t) |
平衡
void balance(AvlNode* & t) |
注:每次balance都会重新矫正这层的高度,因此放在顺序结构的最下层,以便递归时从小到大的进行balance
删除
void Delete(const E&x,AvlNode*& t) |
伸展树(spread tree)
内部节点结构为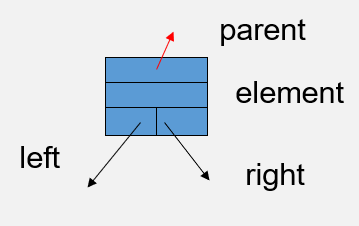
find
假设findR
伸展树的每次find都会使被访问到的节点旋转到根节点


这种旋转,应先旋转Q,P,再R,Q
展开

看上去就像是移动了两个节点(仅对“一字型”而言),其余一致
注:因为伸展树的旋转树是硬转,可能平衡,也可能不平衡,故有时为了把目标节点旋转到根节点的位置,需要补充空节点。其余与AVL一致
插入
即正常插入值后再将其旋转到根上
删除
访问一次该节点,置到根上后删除,取左子树的最大值,展开到根,原本的右子树作为现在的根的右子树
B树
B树相比于二叉树,有更多的子代。
特点
数据项存储在叶上
阶数(order)M表示节点最大的子树数量,因此其最多可以存储M-1个关键字,第i个关键字代表第i+1个子树的最小值
根的儿子数在2~M之间
非叶非根节点的孩子数在⌈ M/2⌉~M之间,关键词数另计
所有叶节点存储的数据项数在⌈ L/2⌉~L之间
B+树

如上图,B+树适用于数据库索引,按键值排序,并且每个叶节点之间用指针链接
B-树
B-树实际上就是B树,我们通常把叶节点用指针链接起来的B-树称为B+树
查找
Find(ElementType K, Btree T){ |
查找过程讲解:
初始化:从树的根节点
T开始,将当前节点B设置为根节点T,即B = T。这个过程是从根开始的,因为 B-树的查找和普通树的查找类似,都是从根节点依次向下递归进入子树进行查找。遍历非叶节点:
- 伪代码中的
while (B is not a leaf)意味着查找过程中只要没有到达叶子节点,就继续向下查找。 - 在非叶节点中,B-树节点包含多个关键字,每个关键字对应一个范围,将关键字
K与当前节点的关键字进行比较,找到K所在的范围,确定Pi,即指向合适子树的指针。 - 找到正确的子树后,将当前节点
B设为该子树的根节点,即B = Pi,继续遍历子树。
- 伪代码中的
进入叶节点:
- 当遍历到叶子节点时,循环结束,此时
B是一个叶子节点。 - B-树的所有数据记录或数据的指针都存储在叶子节点中,因此需要在叶子节点上确认是否包含要查找的关键字
K。
- 当遍历到叶子节点时,循环结束,此时
查找关键字:
- 如果关键字
K存在于当前叶子节点B中,且是第j个关键字,则通过j对应的记录指针找到与K相关的记录。 - 如果在叶子节点中没有找到
K,即关键字不在当前节点中,报告查找失败。
- 如果关键字
B-树查找的核心思想
分层查找:B-树的查找是通过逐层向下,逐渐缩小查找范围的过程。每次查找都通过在非叶节点中找到指向子树的指针,递归地进入对应子树,直到最终找到或确认关键字不存在。
多路分支:每个B-树节点(尤其是非叶节点)通常包含多个关键字,因此每个节点的查找类似于在多个范围中确定属于哪一个范围,并选择相应的子树。
叶子节点存储数据:B-树的叶子节点保存了所有关键字及其相关数据或指针,因此最终查找的结果都会在叶子节点中完成。
插入
Insert(ElementType K, Btree B)
{
find the leaf node LB of B in which K belongs;
if notfull(LB) insert K into LB;
else {
split LB into two nodes LB and LB2 with
j = int((L+1)/2) keys in LB and the rest in LB2;
if ( IsNull(Parent(LB)) )
CreateNewRoot(LB, K[j+1], LB2);
else
InsertInternal(Parent(LB), K[j+1], LB2);
}
}插入过程讲解
找到合适的叶节点:
- 首先,通过B-树的查找过程,找到
K应该插入的叶子节点LB。这和查找操作类似,即从根节点开始,逐步向下寻找正确的叶子节点。
- 首先,通过B-树的查找过程,找到
检查叶子节点是否有空位:
- 如果
LB还没有满,直接将关键字K插入LB中合适的位置。这个步骤相对简单,因为B-树的节点是有序的,插入时需要保持节点内的关键字顺序。
- 如果
叶子节点满时的分裂:
- 如果叶子节点
LB已经满了,则需要进行分裂操作。具体步骤如下:- 将叶子节点
LB分成两个节点LB1和LB2。 - 设
j = ⌊(L+1)/2⌋(向下取整),即计算将原叶子节点中的关键字一分为二的位置。分裂后,LB1保留前j个关键字,剩下的关键字放入新节点LB2中。
- 将叶子节点
- 如果叶子节点
处理父节点:
分裂节点后,需要将中间的关键字(
K[j+1],即分裂过程中跨越两个节点的中间关键字)插入到父节点中,以保持B-树的结构。如果
LB没有父节点,说明LB原来是根节点,这种情况下需要创建一个新的根节点。新的根节点会包含K[j+1]作为它的唯一关键字,并且指向两个子节点LB1和LB2。注:在叶节点以外,所有的关键字只出现一次
如果
LB有父节点,则将K[j+1]插入到LB1的父节点中,并且父节点要处理LB2作为新的子节点的情况。这个过程可能导致父节点再次溢出,从而需要递归地进行分裂和插入操作。
递归处理父节点插入:
- 如果父节点在插入新关键字时再次溢出,那么需要重复上述分裂和插入的过程,直到没有溢出的情况为止。这个过程可能会从叶子节点一直递归到根节点,最终可能会导致整个树的高度增加。
插入的核心思想
局部调整:B-树的插入操作优先在叶子节点进行。如果叶子节点有空位,插入操作只会影响该叶子节点,不需要对树做任何调整。
分裂节点:当节点满时,必须将其分裂为两个节点,并将中间关键字提升到父节点。这种机制确保了B-树的节点不会超过预定的容量上限。
递归调整父节点:如果父节点也因为插入新关键字而满了,同样需要进行分裂,并将中间关键字继续提升。这个过程可能递归到根节点。如果根节点溢出,则需要创建一个新的根节点,树的高度因此增加
注:叶节点与其父节点之间可以存在重复元素,但其他的则不行删除
B-树删除操作的过程
B-树的删除主要包括以下步骤:
找到要删除的关键字所在的节点:
- 通过类似查找操作的方式,从根节点出发,找到包含要删除关键字
K的叶子节点或非叶节点。
- 通过类似查找操作的方式,从根节点出发,找到包含要删除关键字
删除的三种情况: 删除操作根据关键字所在的位置分为三种情况来处理。
情况1:关键字在叶子节点
如果要删除的关键字K在叶子节点,且删除不会导致叶子节点的关键字数目低于最低要求(即至少有 $\lceil m/2 \rceil - 1$ 个关键字,其中m是B-树的阶数),那么可以直接删除该关键字,不需要额外调整。例子:如果叶子节点中有足够的关键字(比如超过最低要求),可以直接删除
K而不破坏B-树的结构。情况2:关键字在非叶节点
如果要删除的关键字K位于非叶节点,那么有两种方法处理:- 用前驱替换:找到
K在该节点左子树中的最大关键字(即K的前驱),将其替换K,并在前驱所在的叶子节点中删除该前驱。 用后继替换:找到
K在该节点右子树中的最小关键字(即K的后继),将其替换K,并在后继所在的叶子节点中删除该后继。删除后递归处理前驱或后继的删除情况。
- 用前驱替换:找到
情况3:关键字在叶子节点中且删除会导致关键字数目不足
如果删除关键字K后,叶子节点中的关键字数目低于最低要求,就需要进行借位或合并操作来恢复B-树的平衡:借位:如果
K的兄弟节点有多于最低要求的关键字,则可以从兄弟节点中借一个关键字。借位过程通过父节点调整关键字,使得父节点的某个关键字“下移”到当前节点,同时从兄弟节点“上移”一个关键字到父节点。合并:如果
K的兄弟节点也只包含最低数量的关键字,则将当前节点和其兄弟节点合并,并将父节点中的一个关键字下移到合并后的节点。合并后,如果父节点关键字数目不足,可能需要对父节点递归进行合并或借位。
如图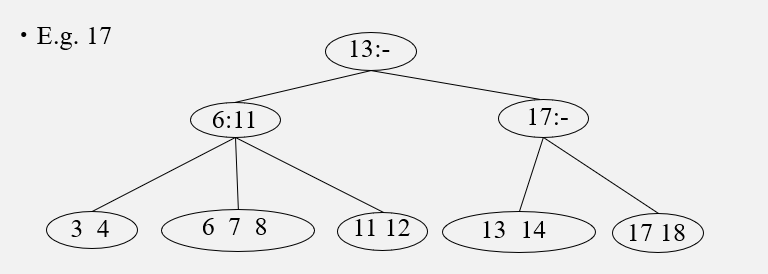
删除17,则13,14,18合并,二级节点的17同时被删除,向其兄弟节点借来11,兄弟的子节点中大于11的索引同步过来。set与map
由于其内核都为红黑树,故放在此处讨论,各方法详见STL
set的实现与map的实现
为该进iterator,使用线索树,在iterator中设置一个bool,不同的值对应左子树还是右子树使用线索的表示
散列
- 散列是一种用于以常数时间插入,删除和查找的技术。
散列通过将数据组使用散列函数得到的值作为索引,以达到类似于数组的效果
散列函数也通常用来加密数据库中的密码,其具有不可逆性,既不能通过散列值得到原本的值
散列是将较大范围的值映射到较小范围内的,这不可避免的会出现带入值不同而散列值一致的情况。
专用于查找与插入为
o(1)的情况
我们将可存储的空间称为槽(slot)搜索
- 成功的搜索:找到键为$K_i=K$的记录;不成功的搜索:未找到
- 完全匹配(exact-match query):查询的键值和给定键值匹配
- 范围查询(range query):查询的键值完全落在给定的键值中
- 自组织列表(self-organizing lists) 使用启发式(heuristic)的策略来决定如何对列表进行重新排序
- 节省空间:直接分配一个大数组意味着要为每个可能的键值分配内存。比如,如果你的键值范围是 0 到 10亿,分配一个长度为 10亿的数组会占用大量的内存,而实际上你可能只需要存储几百个或几千个键值。散列表通过散列函数将键值映射到一个较小的索引空间,因此更加节省空间。
稀疏(spare)
灵活的键类型:如果键不是简单的整数,而是字符串、对象等复杂类型,直接用这些键作为数组索引是不现实的。散列函数可以将这些复杂键映射为一个整数索引,从而适应更灵活的键类型。
更快的查找速度:散列表的查找、插入和删除操作在理想情况下可以达到常数时间复杂度 O(1)O(1)O(1),相比线性查找数组中的元素快得多。散列函数直接计算出索引,不需要遍历数组。
应用
- 作为散列表
- 对比验证信息传输的正确性
- 对比散列值矫正数据错误
- 数据库索引
- cache
- 密码学
用于在RAM上查找数据
散列表(哈希表)
通过键值直接访问的一种数据结构
碰撞(collision)
不同的关键字得到相同的哈希值(hash value)
构造散列函数
直接定址法(注)
哈希值为本身的方法,需要关键字连续且范围较小
平分取中法(mid-square)(注)
将关键字平方后取特定连续位数的一种方法
数字分析法
排除连续关键字中相同的或者具有相同特征的位,取剩余的位合并为一个哈希值
折叠法
将本身较长的关键字分为均匀的几个部分,在将他们自低位对齐后相加得到哈希值
随机值
取关键字的随机函数值作为哈希值
除留余数法
对于表长为m的哈希表,取值p<=m,使hash(k)=k%p;p一般取接近m的素数或m本身
减去法
相当于直接定址法,只不过减去了一个固定的值使得索引可以从较小的值开始,如0,1,2…
基数转换法
将十进制的关键字视为与十互素的进制,再转换为十进制
字符串数值哈希法
适用于关键字使字符串的情况
处理冲突(碰撞)
聚集
由于大部分散列函数的结果从总体上看是不连续且显著集中分布的,故聚集情况常常出现
装填因子
其中$H(key)$为哈希函数,m为表长,$d_i$为增量序列
分类
假定关键字%10的结果为散列函数,若插入时空间已经满了,那么则执行以下的方法,使得重新选址
线性探测
linear probing
增量序列一般固定为1,即$d_i$=1,线性探测倾向于使散列表填满,但这会大大减慢单列表的速度。同时,也会引发一次聚集问题,即散列表中的某个区块全部被占用,此时需要的插入的时间就大大延长了
| 散列地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 未插入 | ||||||||||
| 插入89 | 89 | |||||||||
| 插入18 | 18 | 89 | ||||||||
| 插入49 | 49 | 18 | 89 | |||||||
| 插入58 | 49 | 58 | 18 | 89 | ||||||
| 插入69 | 49 | 58 | 69 | 18 | 19 |
当计算的散列值对应的空间已经满了,那么就在线性探测中使用公式,依次向后移动
平方探测(注)
取增长序列为$d_i=(i\%10)^2$
平方探测可以解决线性探测的一次聚集问题。
有定理:如果使用平方探测,表的大小是素数,且表的一半及以上是空的,那么总能成功插入一个素数。
但这也引发了二次聚集问题。
| 散列地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 未插入 | ||||||||||
| 插入89 | 89 | |||||||||
| 插入18 | 18 | 89 | ||||||||
| 插入49 | 49 | 18 | 89 | |||||||
| 插入58 | 49 | 58 | 18 | 89 | ||||||
| 插入69 | 49 | 58 | 69 | 18 | 89 |
双重哈希
使用哈希值的随机函数取得。
双散列(注)
取增长序列为$d_i=i·H2(key)$,有此,哈希函数hash2的结果不能为0。
对于此方法,算出H2后,用i遍历插入尝试,i的范围是0到散列表的最大值-1。
链地址法
链接列表分开存储
开放定址法是将重复的地址转换为不重复的地址,而此方法将所有重复的地址放在一起。
这种方法的基本思想是把所有哈希地址为i的元素构成一个称为同义词链的单链表,并将其头指针存放在哈希表的第i个单元中。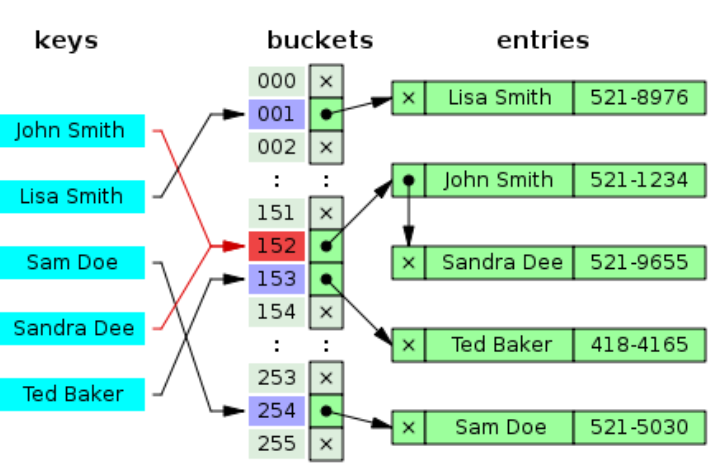
列表头单元格分开链接
将第一条记录放置在单元格内,并设置一个指针以访问下一条同地址的记录。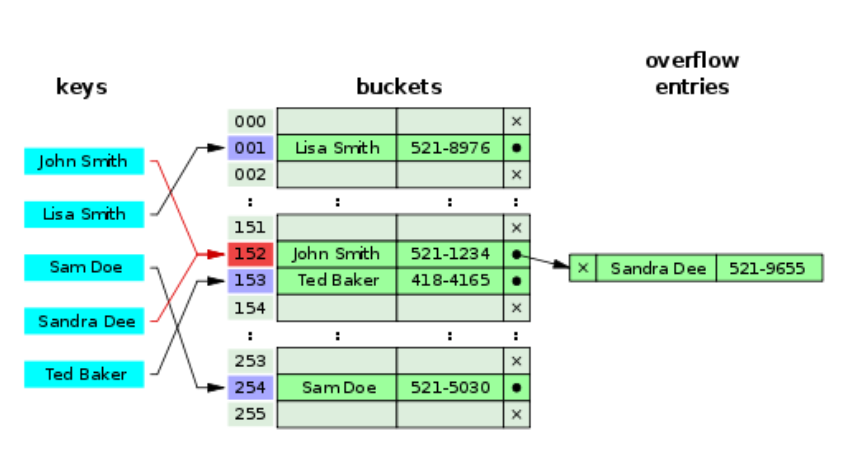
分离链接法
可以将存储的信息放置到链表中,每条链表的代表每个同地址的记录,单元格存放链表的头指针。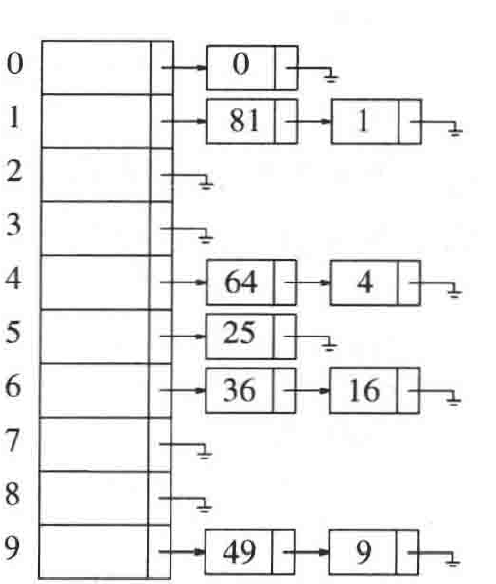
多重哈希法
再哈希法
即当一次哈希函数的计算后发现地址重复,则再次将哈希值带入哈希函数进行计算,直到地址不再重复。此方法可以避免聚集,但计算量大,用时长。
建立公共溢出区
即将重复地址的元素放置到溢出区中。
再散列(rehashing)
顾名思义,当我们认为表的大小足够,不得不补充空间时,使用再散列。再散列将散列表的大小扩展为原大小的两倍以上的第一个素数。
有三种方法判断是否需要再散列。
表到一半满(half full)时再散列
插入失败时在散列
增长因子到达一定值时再散列(推荐)(middle-of-the-road strategy)
完美散列
在分离链接法中,我们知道链表的数量越多,查找所需的时间越少。对于链表的个数M以及项数N,当$M=N^2$时,最小有1/2的概率不会发生冲突,但直接使用这么多的链表不切实际,故使用完美散列,如下图
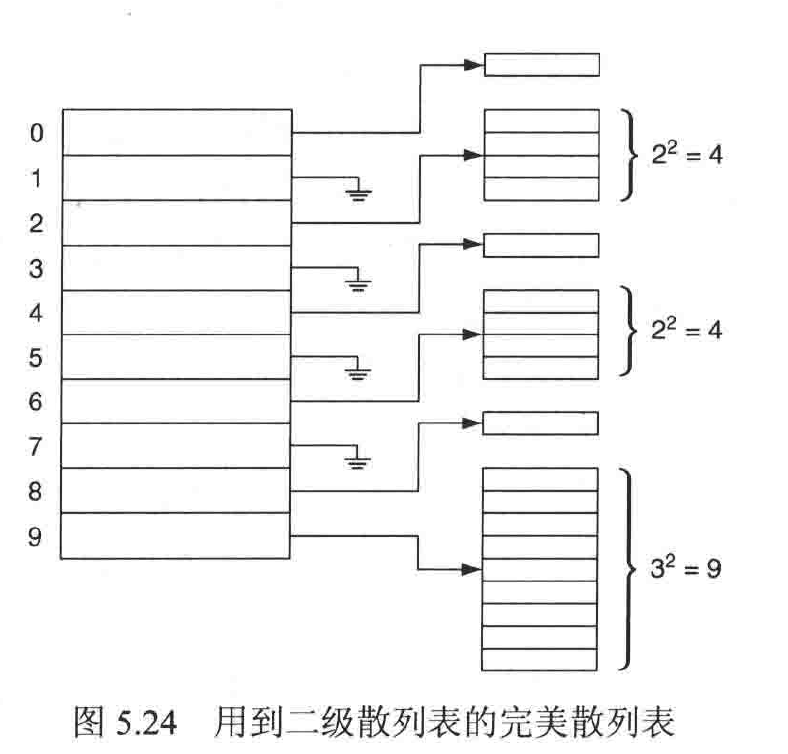
每个单元格中的项数平方后的值为此单元格对应的链表数。这样既能保证较小概率冲突,又能减少链表的数量。
杜鹃散列
在杜鹃散列中,我们维护两个散列表,每个都多于半空,再提供两个散列函数,每个函数都能访问到一个散列表。对于要插入的项,两个散列表各有一个对应的位置可供插入。
步骤
两个散列表分别称之为A表和B表
项先插入A表
若A表对应的是空,则插入;反之,依旧插入,但是原位置的项移动到表二的对应位置
若移入B表的位置也不为空,则依旧放置,原位置的项向A表寻找位置
如下:- 插入A项
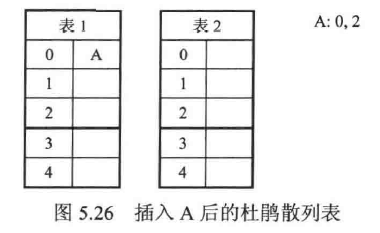
- 插入B项
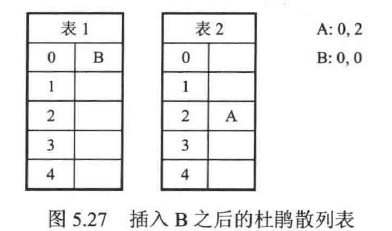
- 插入CDE三项
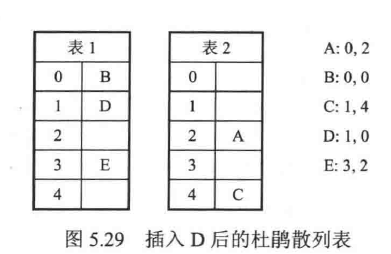
诸如上面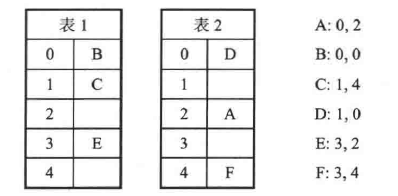
观察发现,六个项中,A表占了3个,B表占了3个,此杜鹃散列最多容纳6个项,若再尝试在(1,2)位置插入G,则会引发循环。
实现及使用时要把装填因子维持在0.5以下实现
留待补充
跳房子散列
跳房子散列维护一个散列表,表中有三个元素:散列值,项,HOP
*散列值:插入一个元素,首先就是要判断其散列值,散列值一致的即可插入
**项:插入该单元的项的名称
Hop*: 跳房子散列给出了一个值MAX_DIST,它标志着一个表中的单元可探测的最大范围,即对于散列值重复的项,可以放置的最大个数。
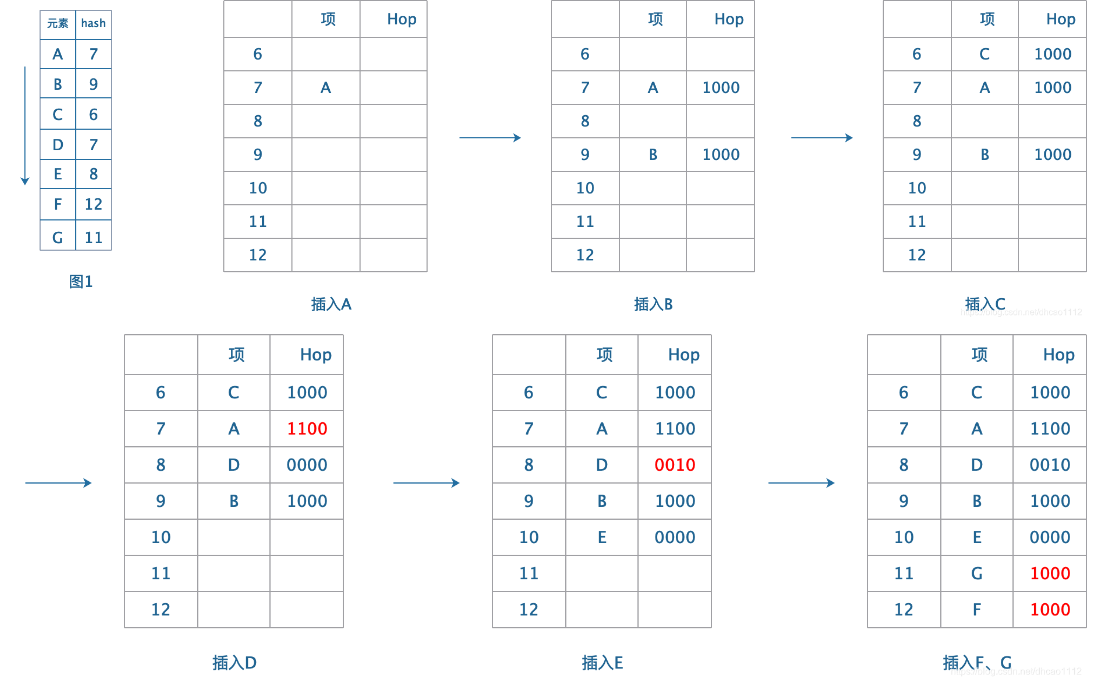
在上图中,此值为4,故Hop格中有4个值,从左到右以依次表示本格,下一格,+2格,+3格的存放情况,为1,表示对应的单元格中存放了一个相同散列值的项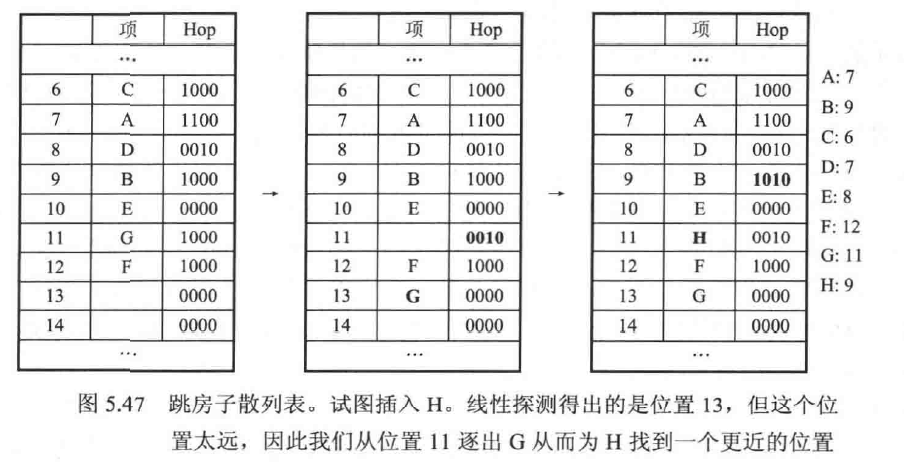
现在尝试模拟此过程:
插入项H,散列值为9。但9被占据,故尝试在其相邻的3格中寻找空位
找不到空位,考虑将这三格中的元素移到三格之外
对于10,存放的不是散列值为10的项,移动会破坏表(因为无法记录),放弃10.
对于11,存在一个放置在本格的项G,可以将他放置在最大值13处,并将Hop修改为0010
插入H,9的Hop更新为1010
通用散列
散列表的性质依赖于
- 散列函数必须常数时间可计算
- 散列函数必须均匀的分布项
可扩散列
*可扩散列(Extendible Hashing)是一种动态哈希表实现方法,特别适用于数据规模变化频繁的场景。它的设计目的是在保持哈希表高效的同时,能够自动扩展或收缩,从而减少重哈希(rehashing)的开销。 维护一个目录:存放项的前n值,当只有1项时,延申出两个块存放项;有n项时以$2^n$的二进制形式增加块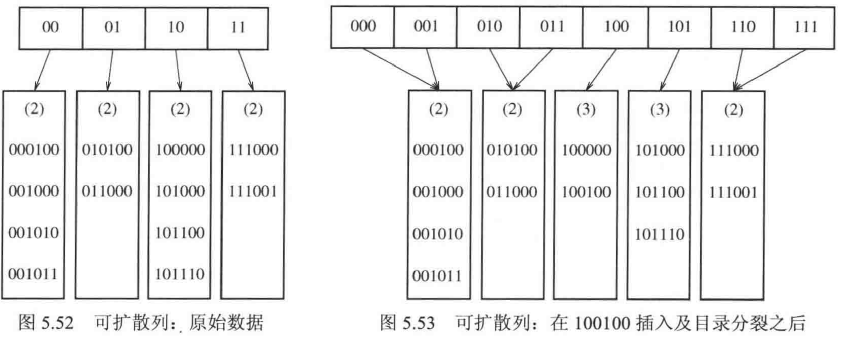
如上,可扩散列还存在一个*深度:表示项中被用于区分的位的数目优先队列
一台电脑面对许多个用户的访问时,会将这些访问放入队列,先发起访问的先使用计算机资源,但是我们希望他能够优先处理完资源较小的请求,因此,设计优先队列。
优先队列会弹出最小的请求,也能对加入的请求排序。二叉堆(Binary Heaps)
堆是一颗完全填满的树,要实现其完全填满的特性,每次插入都要从左往右填满一行再去考虑下一行,如下图所示:
这样实现的二叉堆完全可以实现使用数组表示,而非使用链表。
堆序性质
template <typename Comparable>//一个可比较的变量模板 |
堆的操作
插入(上滤)(insert)
时间 O(log N)
将一个值插入二叉堆,则从最下一层寻找空位,然后以此空位向上寻找合适的位置,若值比插入的大,则交换,否则插入完成。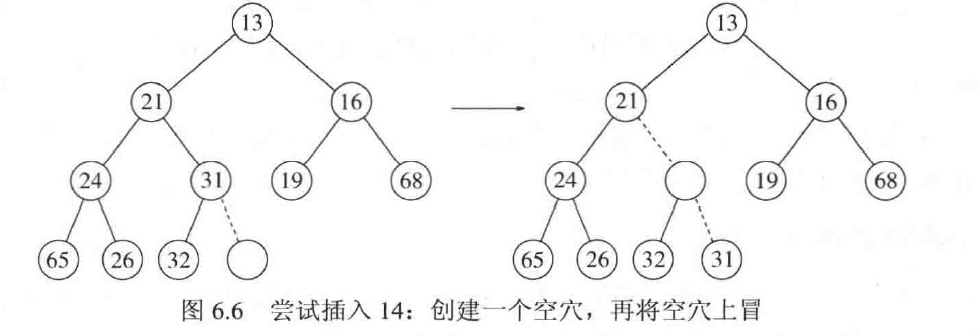
上滤:将插入的值写入0位置,再把hole向上移动,最后写回hole的操作
时间复杂度:最优O(1),最坏(logn+1),平均O(logn)void insert(const Comparable&x)
//此处的起始索引为0,但起始的存储索引为1,原本的计算规则不变
{
if(currentSize==array.size()-1)
array.resize(array.size()*2);
int hole=++currentsize;
Comparable copy=x;
array[0]=std::move(copy);//array[0]是空闲节点,无数据存储
for(;x<array[hole/2];hole/=2)//找到父节点位置
{
array[hole]=std::move(array[hole/2]);//替换
}
array[hole]=std::move(array[0]);
}
删除最小元(deleteMin)
时间O(logN)
将根节点置空,再将最后一个节点提取出来(用来填补被上移的空余)然后向下比对两个子,取最小的上移,直到到达最后一列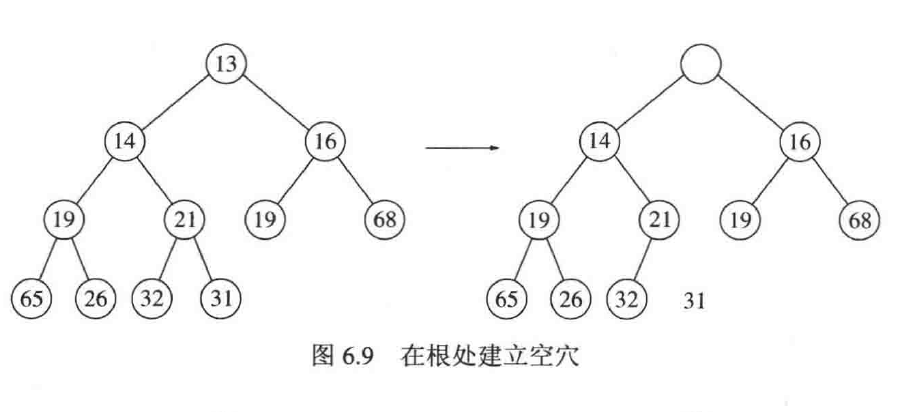
这种方法也叫下滤(percolateDown),即将一个节点向下比较移动的过程。
为了方便记录,我们把删除最小节点和下滤分离
删除最小节点:去除[1]位置的元素,把最后一位移到1的位置,同时currsize—
下滤:根据传入的hole的位置,提取出其中的元素,向下找比他小的节点移动,否则停止,把之前提取出的元素写入现在hole的位置
时间复杂度为:O(堆的深度)
void deleteMin(Comparable & minItem) |
降低节点值(decreaseKey)
decreaseKey(p,k),对节点p的关键字降低K的绝对值,并上滤。
增加节点值(increaseKey)
同上
删除(remove)
remove(p),要将p删除,需要使用上滤将p(假设提前执行了decrease,节点值无穷小)移到根处,在执行deleteMin。
buildHeap(构建堆)
下滤操作从最后一个树叶的父节点递减开始
时间平均O(N),最坏O(NlogN)
void buildHeap() |
先使用完全树直接插入,在使用下滤排序
应用
堆排序
事件模拟
d堆
所有的节点都有d个儿子,在优先队列太大无法装进主存,就可以使用d堆,相当于b树。
左式堆
堆难以实现find和合并(merge),故使用左式堆。左式堆与二叉堆唯一的区别是不平衡,其左树深于右树。
性质
定义零路径长npl(X),表示从X到一个不含有两个儿子的节点的最短路径长。
单节点的npl=0;无节点的npl=-1。
操作
其他操作与二叉树一致,这里讨论合并。
两个左式堆的合并,首先将A堆的右子树插入B堆(B堆的根节点大于A堆),再作为右子树插入A堆,最后为满足左式堆的性质,可能交换两个子树。
斜堆
斜堆与左式堆的差别在于斜堆不对左右子树的深度做要求。
斜堆的主要操作也是合并
合并
二项队列(没讲)
二项队列的插入花费常数时间,其他操作花费O(logN)
二项队列的构建
二项队列由许多个二项树组成,分别由 $B_i$ 表示,其中,i也表示每个树的高度,i从0开始计。这些项数的集合称为森林。如下图所示:
每个二项树的节点数为 $2^i$ ,每个二项树的每个高度的节点数为 $C_{i}^{k},0<=k<=i$ 。
二项队列操作
插入
二项队列的插入由合成大西瓜构成。先得到 $B_0$ (高度为0),随后插入一值得到 $B_1$ (高度为1);再插入两个值,现在有两个 $B_1$ ,因此可以合成 $B_2$ ,诸如此类,如下图所示
其中,大小的比较仍然存在,相同高度的树的合并由下给出
合并
当两个树的高度相同时,二者就可以合并。合并时,取较小的根节点作为新的根节点,另一个树作为子节点插入新的根节点。合并是连锁的,可以(1+1)+2=3。如下图:
删除最小值
先寻找二项队列中最小的根,将对应的二项树从森林中删除,得到新的二项队列 $H’’$ ,然后,将此前的二项树的根节点删除,得到新的二项队列 $H’’$ ,我们对两个二项队列合并即可。
二项队列实现
排序
排序的特征
稳定(stability)
不会破坏相同元素的相对位置关系
就地(in place)
额外空间复杂度:1
插入排序
稳定且就地的
维护一个指针,用来遍历排序的数组,指针每移动一次,就把当前位置的数字一次向前比较,直到插入一个合适的位置,此方法保证此前的数据都是有效的。
实现
template<typename E,typename Comp> |
分析
运行时间上界$O(N^2)$,下界$O(N)$,平均$O(N^2)$。
冒泡排序
稳定且就地
双重循环,每次比较相邻的两值,若最小的循环内未发生交换,则排序成功。template<typename E,typename Comp>
voif bubsort(E A[],int n)
{
for(int i=0;i<n;i++)
{
for(int j=n-1;j>i;j--)
{
if(Comp::prior(A[j],A[j-1]))
swap(A,j,j-1);
}
}
}
自下而上的排序,。
分析
运行时间上界$O(N^2)$,下界$O(N)$(未优化则为$O(N^2)$),平均$O(N^2)$。
选择排序
不稳定,就地
从左到右遍历序列,找到最小值,放置在队首,再循环的找剩下队列的最小值。template<typename E,typenmae Comp>
void selsort(E A[],int n)
{
for(int i=0;i<n;i++)
{
int lowindex=i;
for(int j=n-1;j>i;j--)
{
if(Comp::lt(A[j],A[lowindex]))
lowindex=j
}
swap(A,i,lowindex);
}
}
不断开循环比较,最小的值放在前面,然后缩小范围继续。
分析
运行时间在任何情况下都是$O(N^2)$。

希尔排序(shell)
不稳定但就地
希尔排序使用一个增量序列(increment sequence) $h_k$,每次排序增量序列发生改变,保证$a[i]<=a[i+h_k]$,由此逐渐使$h_k$递减,直到完成排序
大框架上看,希尔排序需要四个循环,一是遍历增量序列,二是序列下所有的子集,三是遍历子集中所有的起点,四是遍历所有起点往前的节点,其中三和四类似于插入排序
实现
template<typename E,typename Comp> |
代码中的取半的序列为希尔增量序列,事实上可能并不可靠。
分析
运行时间上界:$O(N^2)$(使用希尔增量);$O(N^{3/2})$(使用Hibbard增量序列:1,3,7…);$O(N^{4/3})$(使用sedgewick:1,6,19,41….)
平均时间:$O(N^{5/4})$(使用Hibbard增量序列:1,3,7…);$O(N^{7/6})$(使用sedgewick:1,6,19,41….)
堆排序
就地但不稳定
对给出的序列构建MAX堆(大小选取与二叉堆相反),每次执行deletedMax,并把最大值放置在数组中因为下滤而空出的那一位中。由此得到的是由小到大的已排序的数组。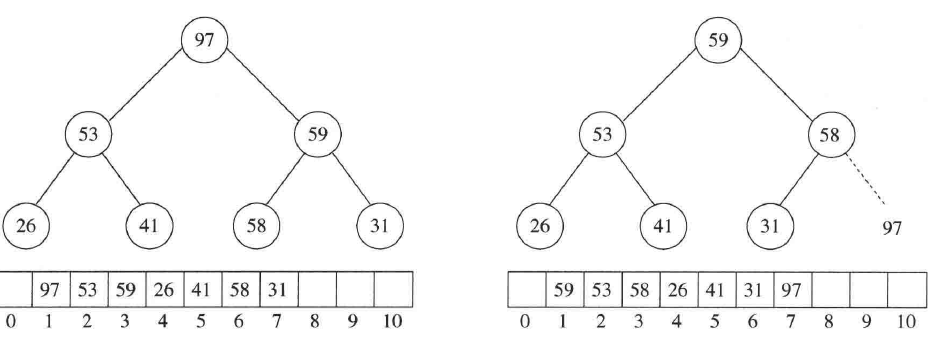
分析
运行时间上界$O(NlogN)$,平均$O(NlogN)$。
归并排序(merge sort)
稳定但不就地
归并排序递归的将序列分为前后一半,排序好后合并两个子序列,直到递归到最大的序列。
实现
实现一
对主函数Mergesort,递归的分解为小数组,在全部递归的组合
对合并函数merge,先合并能合并的,未合并的也一定是已排序好的,直接写入(需要一个辅助数组帮助合并)Mergesort(A[],T[],int left,int right)
{
int mid=(left+right)/2;
if(left<right)//递归
{
Mergesort(A,T,left,mid);
Mergesort(A,T,mid+1,right);
}
Merge(A,T,left,mid+1,rigth);//合并,左开始指针,右开始指针,右结束指针
}
template<typename Comparable>
void merge( vector<Comparable> & a, vector<Comparable> & tmpArray,int leftPos,int rightPos,int rightEnd)//a为待排序的数组,tmpArray为临时数组,leftpos表示a的左侧起始位,rightpos表示a的右侧起始位,rightend表示右侧结束位
{
int leftEnd =rightPos -1;//左侧结束位
int tmpPos =leftPos;//填入临时数组的指针
int numElements = rightEnd - leftPos + 1;//写入临时数组的位数
// Main loop
while( leftPos <= leftEnd && rightPos <= rightEnd)
{
if(a[ leftPos ]<= a[ rightPos ])
tmpArray[ tmpPos++ ]=std::move( a[ leftPos++ ]);
else
tmpArray[ tmpPos++ ]= std::move( a[ rightPos++ ]);
}//取最小的放左边
while( leftPos <=leftEnd)// copy rest of first half
tmpArray[ tmpPos++]=std::move( a[ leftPos++ ]);
while( rightPos <=rightEnd)// Copy rest of right half
tmpArray[ tmpPos++]=std::move( a[ rightPos++ ]);
//由于递归的限制,此后的数据是已经排序的,故直接填入
// Copy tmpArray back
for( int i=0;i<numElements; ++i,--rightEnd )
a[ rightEnd ]=std::move( tmpArray[ rightEnd ]);
//发挥临时数组的作用
}
实现二
使用了小数组进行插入排序的方法,合并的最小单位增大,最后进行合并时使用一个数组的两端合并template <typename E,typename Comp>
void mergesort(E A[], E temp[], int left, int right)
{
if((right-left)<=THRESHOLD)
{
insertionsort<E,Comp>(&A[left], right-left+1);
return;
}//小数组使用插入排序,&传入部分数组和对应长度
//开始合并
int i, j, k, mid = (left+right)/2;
if(left== right)return;
//老套路
mergesort<E, Comp>(A, temp, left, mid);
mergesort<E, Comp>(A, temp, mid+1, right);//Do the merge operation. First copy two halves to temp
//两个部分最终插入排序
for (i=mid; i>=left; i--)
temp[i]= A[i];
//一个数组暂时存储左边部分,方便合并
for (j=1;j<=right-mid; j++)temp[right-j+1]=A[j+mid];//Merge sublists back to A
//再倒叙存储右边部分
for (i=left, j=right, k=left;k<=right; k++)
if (Comp::prior(temp[i],temp[j]))
A[k]= temp[i++];
else A[k]= temp[j--];
//j使用倒序,防止之后插入到原数组时i领先j
}
分析
运行时间上界$O(NlogN)$。
快速排序
就地但不稳定
包含4步:
- 若S中的元素个数为0或1,则直接返回
- 取S中的任意元素v,称之为枢纽元
- 将S中小于等于v的和大于等于v的分为两个子集
- 返回对这两个子集的快速排序。
整体上看,我们只在分集合时进行了排序,且排序由小到大,每次得到枢纽元,以便于合并序列选取枢纽元(pivot)
三数中值
取序列首,尾,中(向下取整)三个值的中间大小值作为枢纽元分割策略
我们取出枢纽元后,将其与序列最后一位元素交换,随后,我们维护两个指针:i与j - i从序列左侧第一位出发,j从序列倒数第二位出发。i先向右比较,若比枢纽元大则停止;若比枢纽元小则向右走一位,直到停止。
- 当i停止时,j项向左走,遇到比枢纽元大的则继续向左走,直到停止;否则停止
- 当i与j都停止时,交换i与j对应的元素
- 当i与j交错,即i>j时,分割完成,将i对应的元素与序列最后一个元素交换,即用枢纽元分割了整个序列。
- 此外,若i与j遇到了与枢纽元相等的元素,则停止
过程如下图:8 1 4 9 6 3 7 5 2 0,选取枢纽元后交换得8 1 4 9 0 3 5 2 7 6
假设输入序列为
小数组
当数组的大小较小时(一般n<10左右)使用插入排序,此时用时比递归的快排更少。快速选择
即查找序列中第k个最小元的问题步骤
- 输入数组s,若s的大小n=1,则将其直接返回
- 选取一个枢纽元
- 将序列分为两部分,若前一个部分数组s1的大小n1>=k,那么在s1中寻找第k个最小值
- 若k=1+n1,则枢纽元恰好是第k个最小值
- 否则,在后一个部分数组s2中寻找第k个最小元
实现
template <typename E,typename Comp> |
最坏情况:$O(N^2)$,平均情况:$O(NlogN)$
排序算法的一般下界&选择问题的决策树下界
此节用决策树证明了只用排序的算法的下界是需要Ω(N log N)次比较。
对手下界
任何基于比较的查找最小元的算法都必然至少使用N-1次比较。
任何同时查找最小项和最大项的基于比较的算法,必然至少使用(3N/2)(取上界)-2次比较
桶式排序和基数排序
桶式排序(Bucket Sort)
使用一个大小至少比序列中最大值大的数组,每次读取序列中的值,就使arry[list[i]]+1,之后读取数组,按值的大小读取即可。
实现
template<typename E,class getKey> |
时间复杂度:O(N)
基数排序(Radix Sort)
当序列的最大数过大,而使用数组太浪费空间时,可以使用基数排序,其也是桶式排序的一部分。一般用于对字符串的比较。
如下图:
从个位数开始比较,最大值不超过9,根据位数使用对应次数的桶排序即可。
但当字符串的长度过长时,基数排序的优先度就不高了
实现
步骤:先按长度排序,在字符串从前到后,字符位数从后往前的排序,每次排序过后重新写入原数组void radixSort(std::vector<std::string> &arr, int maxLen) {
const int BUCKETS = 256;//桶大小
std::vector<std::vector<std::string>> wordsByLength(maxLen +1);
//初始按长度先排序
std::vector<std::vector<std::string>> buckets(BUCKETS);
//桶排序
for (std::string &s : arr)
wordsByLength[s.length()].push_back(std::move(s));
//按长度塞入数组
int idx = 0;
for (auto &wordList : wordsByLength)
for (std::string &s : wordList)
arr[idx++] = std::move(s);
//再写回原数组
int startingIndex = arr.size();
for (int pos = maxLen - 1; pos >= 0; --pos) {
startingIndex -= wordsByLength[pos + 1].size();
//表示从对应长度区间的字符串开始排序
//pos表示访问字符串的哪一位,字典序的判断应是自后到前的
for (int i = startingIndex; i < arr.size(); ++i)
buckets[arr[i][pos]].push_back(std::move(arr[i]));
//按pos指向的位进行桶排序
idx = startingIndex;
for (auto &thisBucket : buckets) {
for (std::string &s : thisBucket)
arr[idx++] = std::move(s);//写回原数组
thisBucket.clear();//清空,准备下次桶排序
}
}
}
此算法可以理解为,先对字符串按长度从小到大排序,再从最后一位向第一位以桶排序进行,若有位数小的,用空格补齐。
时间复杂度:Ω(Nlog N)
外部排序
磁带等辅助存储设备无法直接寻址,此前的排序算法都是基于元素可直接访问的基础而设计的,故需要额外的外部排序算法对磁盘中的数据进行排序
简单算法
在此算法中,我们使用归并排序的合并算法。
假设我们有四个磁带,$T_{a1},T_{a2},T_{b1},T_{b2}$,可分别表示输出或输入磁带,设数据最先存储在$T_{a1}$中,则:
- 假设内存一次最多容纳和排序M个元素,我们每次从$T_{a1}$中取出M个元素,排序好后交替的放在$T_{b1},T_{b2}$中,如下图

- 现在所有的元素都已经排序好了,于是进行合并,我们每次从$T_{b1},T_{b2}$中取出一组顺串(已排序的序列组),合并且交替记录在$T_{a1},T_{a2}$中,直到$T_{b1},T_{b2}$中没有元素,如下图:

- 再将$T_{a1},T_{a2}$中的一组顺串合并,交替的记录在$T_{b1},T_{b2}$中,如下图:

- 最后一次合并,记录在$T_{a1}$中,如下图:

在此算法中,合并是找两个数据的最小值,然后直接写入磁带,同时对应的输入磁带向前前进一位。
平均时间:$log_2^{需要排序的趟数}$
替换选择算法(replacement selection algorithm)
一次能排序的对的长度为内存的两倍
应用在初始排序,有数据成员LAST,表示队列最后一个已经排序的索引
步骤:
- 弹出队列根的元素,产生空格
- 若插入的元素大于弹出的元素,就把插入的元素写入空格;反之把LAST的元素写入空格,把插入的元素写入LAST,LAST—;
- 对根节点下滤
多路合并
在简单算法中,我们受限于磁盘的数量,一次只在2个磁盘中交互的合并(2路合并),这会增加外部排序的时间,假设我们有多个磁盘用于排序,则引入k路合并。
我们使用优先队列来对磁盘指针指向的元素排序,每次使用deleteMin排出最小元素,写入输入磁盘后对应的输入磁盘前进。
假设我们现在使用3路合并: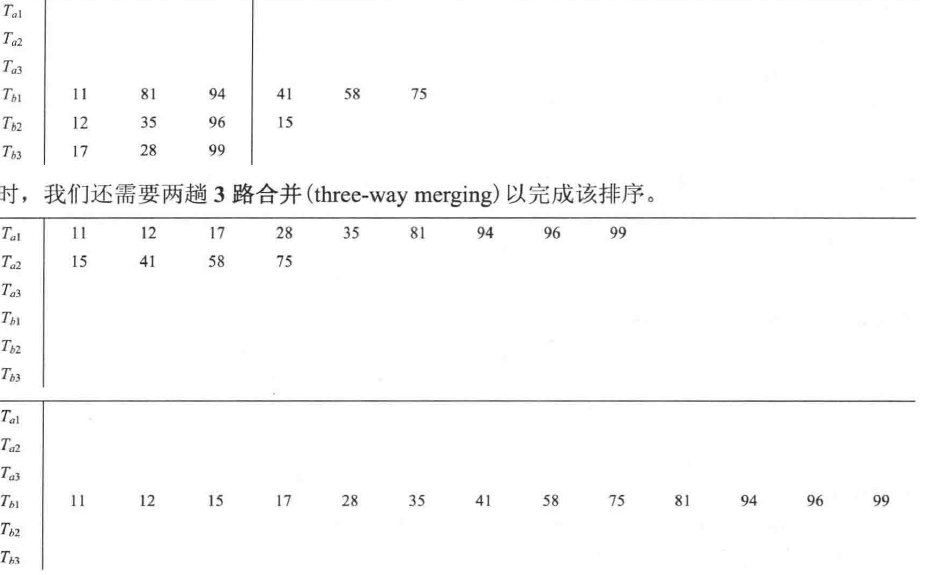
平均时间:$log_k^{需要排序的趟数}$多相合并
我们考虑使用更少的磁盘数,完成相同的工作,考虑使用三个磁带完成2路合并:
假设我们在磁盘$T_1$上存储34个输入顺串,使用斐波那契数列的倒叙方法,不平均的把34个顺串分配21个到$T_2$上,分配13个到$T_3$上,再合并到$T_1$上;每次合并保证有两个盘没空,彼此合并后得差,再合并,直到消为1。
不相交集类
本节研究将一个集合通过等价关系划分为交集为空集的几个子集间的各种快捷操作。这些子集称为等价类。对于集合中的元素,我们使用find寻找其类名(或是能唯一表示此等价类的属性),使用union将两个不在一个等价类中的元素合并到一个类中。class DisjSets{
public:
explicit DisjSets( int numElements );
int find( int x ) const;
int find( int x );
void unionSets( int root1, int root2 );
private:
vector<int> s;
};
DisjSets::DisjSets( int numElements ) : s{ numElements, - 1 }
{
}
等价关系
自反的,对称的,可传递的
等价关系把集合划分为数个不同的子集。考虑关系a与b为同性,把人群划分为男女两个子集。
联机(dynamic)/脱机
联机表示find操作必须当场给出
脱机表示find操作在考虑全部的union操作后才能给出
普通求并实现
在这种实现中,我们使用森林的概念,每个元素起初都是一个单独的树。此外,我们维护一个数组,来存放每个元素的树的根。
如下图: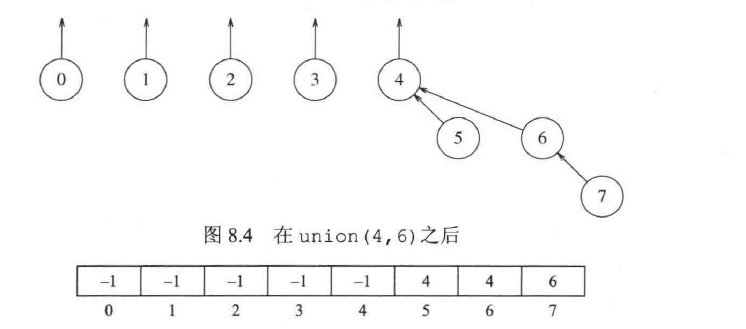
union
我们把一个元素的树的根作为子树加到另一个元素下,同时跟新数组中记录根信息的内容。
实现如下:void DisjSets::unionSets( int root1, int root2 )
{
s[ root2 ] = root1;
}
find
我们通过数组直接寻找其根信息,直到找到-1的节点,说明此元素可以直接表示一个等价类
实现:
int DisjSets::find( int x ) const
{
if( s[ x ] < 0 )
return x;
else
return find( s[ x ] );
}
灵巧求并算法
按大小求并
我们使用按大小求并的思想,合并时寻找两个树中大小较小的那个作为较大的树的子树。
大小表示数中节点的数目
如下图所示的合并操作: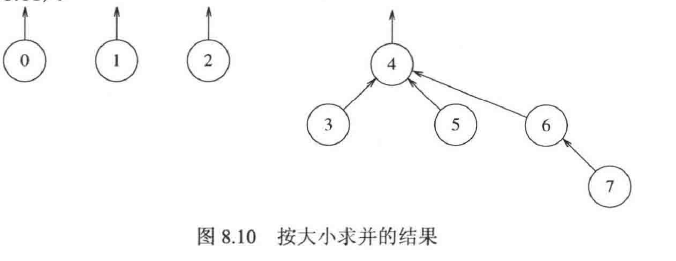
维护的数组为:
其中,正数表示根,负数表示节点数
按高度求并
我们使用按高度求并的思想,追踪每个树的高度而非大小,合并会使高度小的树成为高度大的子树。
例子结果与按大小求并一致,但数组不同:
负数为高度-1
实现
一般实现按高度求并的部分:void DisjSets::unionSets( int root1, int root2 )
{
if( s[ root2 ] < s[ root1 ] ) // root2更深
s[ root1 ] = root2; // root2为新根
else {
if( s[ root1 ] == s[ root2 ] //
--s[ root1 ];
s[ root2 ] = root1; // 无论小于还是等于,root1为新根
}
}
路径压缩
此前我们使用find时,都是递归的获取根的信息,但使用路径压缩后,我们将find的结果直接赋值到每次递归查找根节点的数组中,这样,可以使用原本的元素直接按数组查找到根值。int DisjSets::find( int x )
{
if( s[ x ] < 0 )
return x;
else
return s[ x ] = find( s[ x ] );//使用=
}
例子
以课本构建迷宫为例,每个单元表示集合的一个元素,随机的选取边拆除以连接两个元素对应的等价类,直到起点与终点对应的等价类被合并。
此外,若墙未拆除且两元素在一个等价类中,那么就不拆除此墙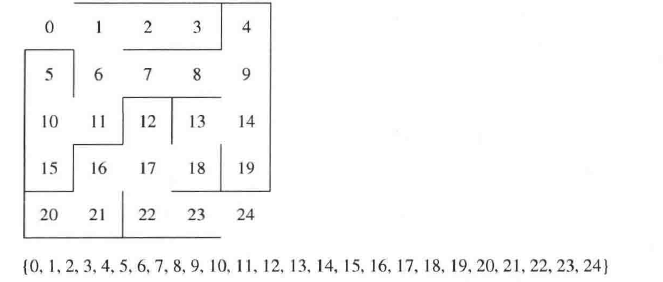
考试中此类型的题离不开两点:
- 集合的合并,能够将题目中的元素抽出以表示集合的概念
- 集合的连通,是合并之后联通,有此概念的一般使用并查集解决
图论算法
定义
- 一个图$G=(V,E)$由顶点(node/vertices) 集V 和 边(edge/arcs)集E构成,一对点对构成了一条边,有时也称为 弧。
- 边有方向的图称为有向图。
- 有的图的边会附带数值,称之为权(weight)。
- 路径(path) 为图中的首尾相联的点序列,其 长 为路径上的边数,若有直接回到自身的路径${v,v}$,则称为环(loop),简单路径指路径中无相同节点,除了首尾。
- 有向图中若有路径长度至少为1,且首尾节点一致的路径,则称为圈(circul),若此路径是简单路径,则此圈也称为简单圈。若一个有向图无圈,则称为无圈的(DAG)。
- 在无向图中,圈要求路径互异,且长度至少为一。
- 有向图中,若每两个节点都有一条路径,则称此有向图是强联通的,若此有向图的无向图的每对节点都有路径,则称此无向图是弱连通的。
- 无向图中,若每对节点都有路径,则称为连通的
- 在有向图中每个顶点都有入度(deg-)(指向该点的边的对应边的数目)和出度(deg+)(此点指向其他点的边数目)。
注:弧指两个顶点之间的连线,路径则不局限于此图的表示
邻接矩阵(adjacency matrix)
对一个有n个节点的图,我们创建一个$n\times n$的矩阵,若两点之间有边,则其置为1,反之为0
对有向图来说,若有从a指向b的边,则在(a,b)中将值置为1。
有时也可以用其权值替代1。
若图是稠密的,则使用邻接矩阵更好
邻接表(adjacency list)
对图中的每个节点a,若有一条边使其与另一个顶点b相联,则将其放入表中a的邻接边中。
若在有向图中,由节点a指向其他节点的边加入a的邻接表
若图是稀疏的,则使用邻接表更合适。
存储
假设节点标签2byte,指针4byte,权值2byte
则:
- 邻接矩阵需要$2V^2byte$
- 邻接表需要$4V+8Ebyte$(有向图),$4V+8*2E$byte(无向图)
方法
一般使用first()获取对应节点的首个邻接元素,next(v’)获得节点v的邻接节点v’后的第一个节点
实现
邻接表
先是定义edge,包括了节点表示和边的权值,指针由模板类list实现;而后定义邻接表类,包括edge的二级指针,节点数,边数和访问状态数组Class Edge
{
int vert;
//节点
int wt;
//权值
Public:
Edge() { vert = -1; wt = -1; }
Edge(int v, int w) {vert = v, wt = w; }
int vertex() {return vert; }
int weight() {return wt; }
}
class Graphl: public Graph
{
private:
List<Edge>** vertex;
//开二维指针
int numVertex, numEdge;
//表示节点和边的数量
int *mark;
//标志数组,表示此节点是否访问过
public:
void Init(int n)
{
int i;
numVertex = n;
numEdge = 0;
mark = new int[n];
for (i=0; i<numVertex; i++)
mark[i] = UNVISITED;
vertex = (List<Edge>**) new List<Edge>*[numVertex];
for (i=0; i<numVertex; i++)
vertex[i] = new Llist<Edge>();
}
int first(int v)
{
if (vertex[v]->length() == 0) //return V’s Llist size
return numVertex;
//表示无此节点
vertex[v]->moveToStart();
//list的方法
Edge it = vertex[v]->getValue();
return it.vertex();
}
int next(int v, int w)
{ //get v’s next neighbor after w
Edge it;
if (isEdge(v, w))
{
if ((vertex[v]->currPos()+1) < vertex[v]->length())
{
vertex[v]->next();
it = vertex[v]->getValue();
return it.vertex();
}
}
return n(); //no neighbor
}
bool IsEdge(int v1, int v2)
//判断节点V1是否存在节点v2
{
for(vertex[v1]->moveToStart(); vertex[v1]-> currPos() < vertex[v1]->length(); vertex[v1]->next())
{
Edge it;
it = vertex[v1]->getValue();
if(it.GetVertex() == v2)
return true;
}
return false;
}
邻接矩阵
同理,只有数组改变存储形态class Graphm: public Graph
{
Private:
int numVertex, numEdge; //#vertices & #edges
int **matrix; //Pointer to adjacency matrix
int *mark; //Pointer to mark array
public:
void Init(int n)
{ //Initialize the graph
int i;
numVertex = n;
numEdge = 0;
mark = new int[n]; //Initialize mark array
for (i=0; i<numVertex; i++)
mark[i] = UNVISITED;
matrix = (int**) new int*[numVertex]; //create
for (i=0; i<numVertex; i++)
matrix[i] = new int[numVertex];
for (i=0; i<numVertex; i++) //Initial to 0 weights
for (int j=0; j<numVertex; j++)
matrix[i][j] = 0;
}
int n() { return numVertex; } //#vertices
int e() { return numEdge; } //#edges
int first(int v)
{ //return first neighbor of v
for (int i=0; i<numVertex; i++)
if (matrix[v][i] != 0) return i;
return numVertex; // Not found
}
int next(int v, int w)
{
for(int i=w+1; i<numVertex; i++)
if (matrix[v][i] != 0) return i;
return numVertex;
}
拓扑排序
对有向无圈图,有拓扑排序:若一个点先于另一个点,则在图中我们把此点放置在前段。
如图: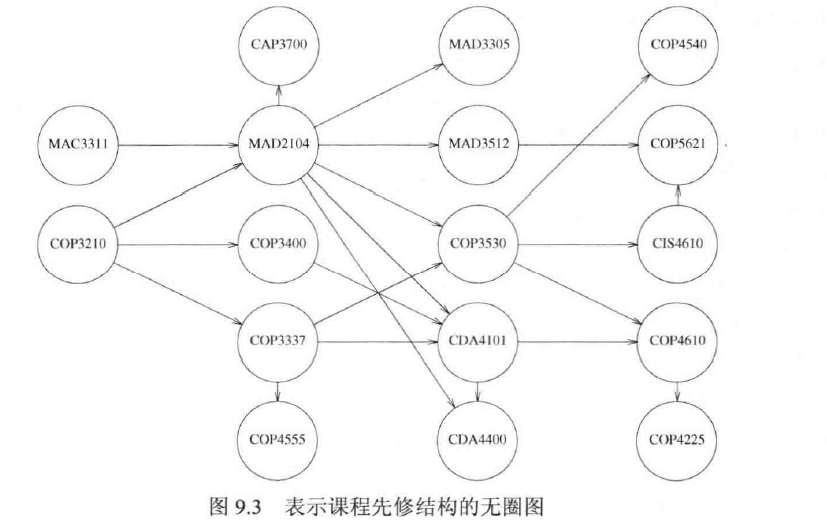
拓扑排序不唯一
实现
以queue为基础的实现
void topsort(Graph* G, Queue<int>* Q)
{
int InDgree[G->n()];
int v, w;
for (v=0; v<G->n(); v++) InDgree[v] = 0; //初始化入度
for (v=0; v<G->n(); v++)
for (w=G->first(v); w<G->n(); w=G->next(v,w))//邻接
InDgree [w]++; // 有一个入度
for (v=0; v<G->n(); v++)
if (InDgree[v] == 0)
Q->enqueue(v);//入队
while (Q->length() != 0)
{
v = Q->dequeue();//出队
printout(v);
for (w=G->first(v); w<G->n(); w=G->next(v,w)) {
InDgree[w]--; //删除对应边
if (InDgree[w] == 0)
Q->enqueue(w);//入队
}
}
}
使用DFS思想的实现void topsort(Graph* G) {
int i;
for (i=0; i<G->n(); i++) // Initialize Mark
G->setMark(i, UNVISITED);
for (i=0; i<G->n(); i++) // Process vertices
if (G->getMark(i) == UNVISITED)
tophelp(G, i); // Call helper
}
void tophelp(Graph* G, int v) { // Process v
G->setMark(v, VISITED);
for (int w=G->first(v); w<G->n(); w=G->next(v,w))
if (G->getMark(w) == UNVISITED)
tophelp(G, w);
printout(v); // output v
}
打印出的即为拓扑排序的反序
遍历
前提
保证每个节点不能走超过两次void graphTraverse(Graph* G)
{
int v;
for (v=0; v<G->n(); v++)
{
G->setMark(v, UNVISITED);
} // Initialize
for (v=0; v<G->n(); v++)
if (G->getMark(v) == UNVISITED)
doTraverse(G, v);
}
深度优先(DFS)
使用堆栈实现,从最深处向最浅处递归Main
{
i : integer //int i
for i = 1 to n do M[i] := 0; //连接分量数组M,连接分量一致表示两个节点可以相联
label := 1;赋值
for i = 1 to n do
if M[i] = 0 then DFS(G,M,i,label); //若无记号,则去搜索
label := label + 1; //寻找下一个节点群
}
DFS(G[]: node ptr array, M[]: int array, i,label: int)
{
v : node pointer; //节点指针
M[i] := label;//标记
v := G[i]; // i的第一个邻居
while v != null do // 直到无i的未标记邻居
if M[v.index] = 0 then DFS(G,M,v.index,label);//递归
v := v.next; // 下一个邻居
假如此图有n个节点,m个边,则DFS的时间复杂度为O(n+m)
广度优先(BFS)
使用队列实现,从最浅处向最深处探索void BFS(Graph* G, int start, Queue<int>*Q)
{
int v, w;
Q->enqueue(start);//初始节点入栈
G->setMark(start, VISITED);//标记
while (Q->length() != 0)//无节点可以加入时
{
v = Q->dequeue();//出队列
PreVisit(G, v);//留白
for(w=G->first(v); w<G->n(); w=G->next(v,w))//依次找邻居
if (G->getMark(w) == UNVISITED)
{
G->setMark(w, VISITED);//标记
Q->enqueue(w);//入队
}
}
}
最短路径算法
无权最短路径
此中情况中我们只需要研究如何找到边数最少的路径,显然我们可以给边赋权值1。
如下图所示: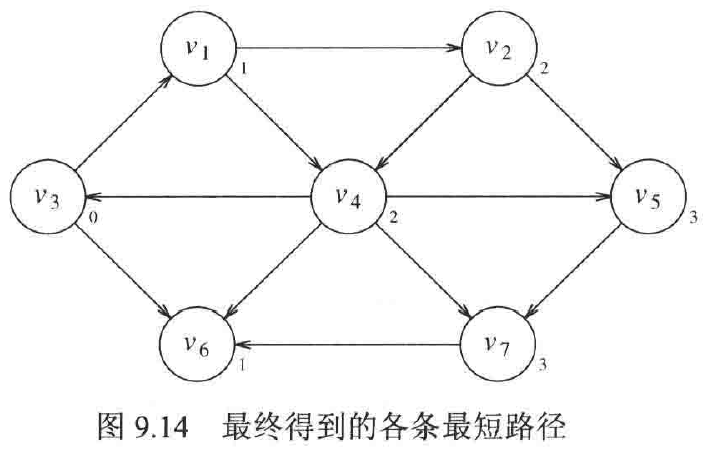
void Graph::unweighted(Vertexs) |
有权最短路径(无负值)(Dijkstra算法)
我们使用优先队列找到权值和最小的那个节点作为下一个确定的点,再为每个节点设置是否确定为最小路径的变量,其余的思路不变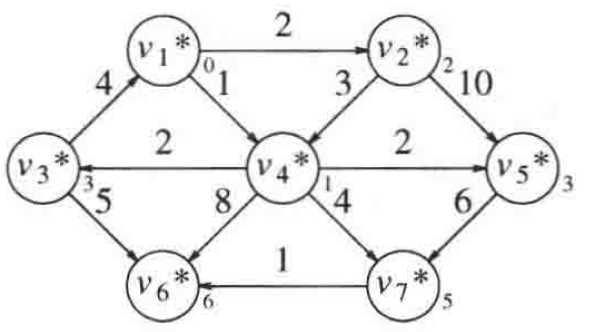
实现一,复杂度$O(n^2)$void Dijkstra(Graph* G, int* D, int s)
{
int i, v, w;
for (int i=0; i<G->n(); i++)
D[i] = INFINITY;//距离无穷大
D[s] = 0;//起点
for (i=0; i<G->n(); i++)
{
v = minVertex(G, D); //寻找未标记的最短距离顶点
if (D[v] == INFINITY) return; //但此点不与起点相连
G->setMark(v, VISITED);//标记
for (w=G->first(v); w<G->n(); w = G->next(v,w))
if (G->getMark(w) == UNVISITED)
if (D[w] > (D[v] + G->weight(v, w)))
D[w] = D[v] + G->weight(v, w);//更新路径长度
}
}
int minVertex(Graph* G, int* D)
{
int i, v = -1;
for (i=0; i<G->n(); i++)
if (G->getMark(i) == UNVISITED)
{
v = i;
break;
}//找到一个对比对象即可
for (i++; i<G->n(); i++)
if ((G->getMark(i) == UNVISITED) && (D[i] < D[v]))//在未标记的节点中找距离比v小的
v = i;//替换
return v;
实现二:使用最小堆找出最小元素,复杂度$O((|V|+|E|)log|E|)$Class DijkElem
{
Public:
int vertex, distance;
DijkElem() {vertex = -1; distance = -1;}
DijkElem(int v, int d) {vertex = v; distance = d};
};
void Dijkstra(Graph* G, int* D, int s) {
int i, v, w;
DijkElem temp;
DijkElem E[G->e()];
for (int i=0; i<G->n(); i++)
D[i] = INFINITY;//距离无穷大
D[s] = 0;//起始节点
temp.distance = 0;
temp.vertex = s;
E[0] = temp;
heap<DijkElem, DDComp> H(E, 1, G->e());
for (i=0; i<G->n(); i++)
{
do
{
if(H.size() == 0) return; // 为空
temp = H.removefirst(); //deletemin
v = temp.vertex;
} while (G->getMark(v) == VISITED);//找到值最小的未标记顶点
G->setMark(v, VISITED); //标记
if (D[v] == INFINITY) return; //不相连顶点
for(w=G->first(v); w<G->n(); w=G->next(v,w))
if (G->getMark(w) == UNVISITED)//未标记的邻接
if (D[w] > (D[v] + G->weight(v, w))) {
D[w] = D[v] + G->weight(v, w);
temp.distance = D[w]; temp.vertex = w;
// Insert new distance in heap
H.insert(temp);
}
//此循环用于更新邻接顶点的值
}
}
具有负值的图
若图的权值可为负,则以上的两种算法不再适用,我们结合前两种算法得出新解:
不标记节点的记录状态,循环将一直继续void Graph::weightedNegative( Vertexs
{
Queue<Vertex> q;
for each Vertex v
v.dist =INFINITY;
s.dist =0;
q.enqueue(s);
while( !q.isEmpty())
{
Vertexv=q.dequeue();
for each Vertex w adjacent to y
if( v.dist + cvw<w.dist )
{
w.dist=v.dist+cvw;
w.path=v;
if( wis not already in g)q.enqueue( w);
}
}
}
无圈图(貌似不考)
若已知图是无圈的,则可以再改进Dijkstra算法,无圈图一般应用再方向唯一的情景中,如滑雪只能向下,自发的化学反应只能释放能量
关键路径分析法
我们将事件与其需要的时间排列为一张图,此图必须是无圈(因为后置任务不能提前完成)。
时间节点图
我们对关键路径分析中得到的图转化为时间节点图,此图可用来规划并行任务的执行时间等(规定若两个事件没有直接或间接相联就可以并行)
最早完成时间
我们计算每个任务完成(包括此任务的先决任务)的最短时间,即每个任务间没有缓冲时间
最晚完成时间
我们计算不影响最早完成时间下的每个事件都能完成的情况,即我们对每个节点尽可能的留出缓冲时间
缓冲时间
我们计算为了最短时间完成任务,每个任务可以留出的缓冲时间
生成树
需要削减图的边数或增加边数,使得原无向图有边数=节点数-1
最小生成树
Prim算法
使用在无向图上,类似于最短路径的算法,只在画边上有不同,边长度不再累加,二而是直接取边权。
需要考虑第一个节点的选择是否是随机的,最后的结果唯一(若无权值相同的边)void Prim(Graph* G, int* D, int s) //s是起始点
{
int V[G->n()]; // store lowest cost vertex
int i, w;
for (int i=0; i<G->n(); i++) // Initialize
D[i] = INFINITY; // cost
D[s] = 0;
for (i=0; i<G->n(); i++) {
int v = minVertex(G, D);
G->setMark(v, VISITED);
if (v != s)
AddEdgetoMST(V[v], v); //把前置节点和当前节点的边接入MST
if (D[v] == INFINITY) return; //unreachable vertices
for (w=G->first(v); w<G->n(); w=G->next(v,w))
if (G->getMark(w) == UNVISITED)
if (D[w] > G->weight(v,w)) {
D[w] = G->weight(v,w); //Update cost
V[w] = v; // 更新前置节点
}
}
}
Kruskal算法
使用并查集的方法,枚举每个最小的边,在不出现圈的情况下加入此边,否则放弃且不在考虑
除非有权值相同的边,否则结果唯一vector<Edge> kruskal( vector<Edge> edges, int numVertices )
{
DisjSets ds{ numVertices };
priority_queue pq{ edges };//优先队列
vector<Edge> mst;
while( mst.size( ) != numVertices - 1 )//树的边数总比其节点数少1
{
Edge e = pq.pop( ); // Edge e = (u, v)
SetType uset = ds.find( e.getu( ) );
SetType vset = ds.find( e.getv( ) );
if( uset != vset )两集合不相等
{
// Accept the edge
mst.push_back( e );
ds.union( uset, vset );
}
}
return mst;
}


